Question
Question: Simplify the following expression: $7-\frac{1}{2}\left[-log(10^{-5})\right]-\frac{1}{2}log(0.02)$ ...
Simplify the following expression:
7−21[−log(10−5)]−21log(0.02)
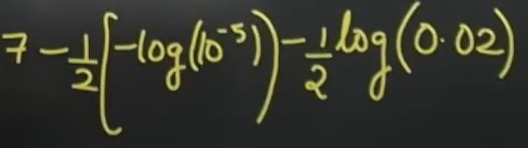
211−log(2)
Solution
The given expression is 7−21[−log(10−5)]−21log(0.02). We assume the logarithm is base 10, i.e., log(x)=log10(x).
We use the following properties of logarithms:
- log(ab)=b⋅log(a)
- log(a⋅b)=log(a)+log(b)
- log(ba)=log(a)−log(b)
- log(10)=1
Let's simplify the expression step by step:
7−21×(−1)×log(10−5)−21log(0.02) =7+21log(10−5)−21log(0.02)
Using property 1, log(10−5)=−5⋅log(10). Since log(10)=1, log(10−5)=−5⋅1=−5.
Substitute this into the expression:
7+21(−5)−21log(0.02) =7−25−21log(0.02)
Now, let's simplify log(0.02).
0.02=1002=501. Using property 3, log(0.02)=log(501)=log(1)−log(50). Since log(1)=0, log(0.02)=0−log(50)=−log(50).
Substitute this back into the expression:
7−25−21(−log(50)) =7−25+21log(50)
Now, let's simplify log(50).
50=5×10. Using property 2, log(50)=log(5×10)=log(5)+log(10). Since log(10)=1, log(50)=log(5)+1.
Substitute this back into the expression:
7−25+21(log(5)+1) =7−25+21log(5)+21
Combine the constant terms:
7−25+21=7+(21−5)=7+(2−4)=7−2=5.
So the expression simplifies to:
5+21log(5).
Alternatively, we can write log(5)=log(210)=log(10)−log(2)=1−log(2).
Substituting this into the expression:
5+21(1−log(2)) =5+21−21log(2) =210+1−21log(2) =211−21log(2) =211−log(2).
Therefore, the final answer is 211−log(2).
