Solveeit Logo
Login

Question

Question: For k≠-1, the area of the triangle formed by $(x_1,y_1), (x_2,y_2), (\frac{kx_1+x_2}{k+1}, \frac{ky_...

For k≠-1, the area of the triangle formed by (x1,y1),(x2,y2),(kx1+x2k+1,ky1+y2k+1)(x_1,y_1), (x_2,y_2), (\frac{kx_1+x_2}{k+1}, \frac{ky_1+y_2}{k+1}) is

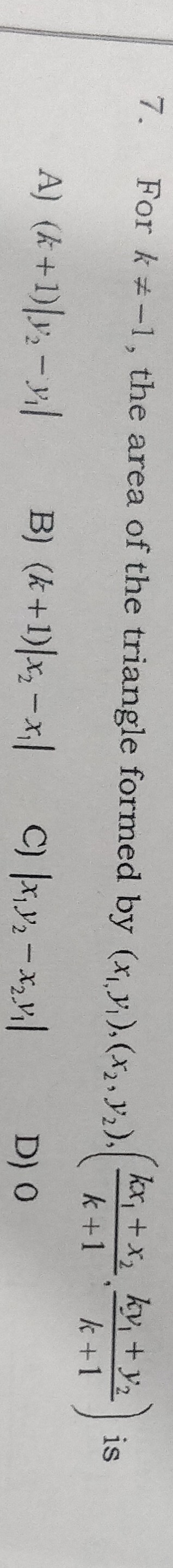
A

(k+1)∣y2−y1∣(k+1)|y_2-y_1|

B

(k+1)∣x2−x1∣(k+1)|x_2-x_1|

C

∣x2−x1∣|x_2-x_1|

D

0

Answer

0

Explanation

Solution

The third point is given by

(kx1+x2k+1, ky1+y2k+1)\left(\frac{kx_1+x_2}{k+1},\,\frac{ky_1+y_2}{k+1}\right)

which is a weighted average of (x1,y1)(x_1, y_1) and (x2,y2)(x_2, y_2). This implies it lies on the line joining these two points. Hence, the three points are collinear, and the area of the triangle they form is zero.