Question

Find the sum of the following infinite series:

$1+\frac{2}{10}+\frac{3}{10^2}+\frac{7}{10^3}+\frac{2}{10^4}+\frac{3}{10^5}+\frac{7}{10^6}+\frac{2}{10^7}+\frac{3}{10^8}+\frac{7}{10^9}+...$

Answer 1

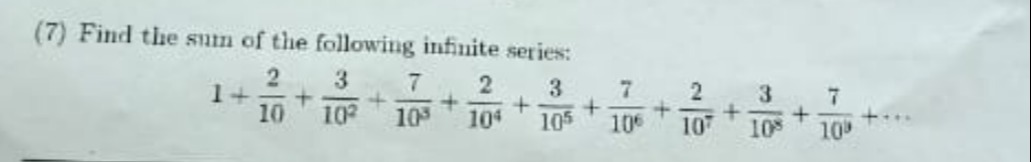
The sum of the infinite series is $\frac{412}{333}$.

Answer 2

The given infinite series is: $S = 1+\frac{2}{10}+\frac{3}{10^2}+\frac{7}{10^3}+\frac{2}{10^4}+\frac{3}{10^5}+\frac{7}{10^6}+\frac{2}{10^7}+\frac{3}{10^8}+\frac{7}{10^9}+...$

1. Identify the pattern: Observe the numerators and denominators. The denominators are powers of 10. The numerators, starting from the second term, follow a repeating pattern: 2, 3, 7, 2, 3, 7, ... This means the series can be written as: $S = 1 + \left(\frac{2}{10}+\frac{3}{10^2}+\frac{7}{10^3}\right) + \left(\frac{2}{10^4}+\frac{3}{10^5}+\frac{7}{10^6}\right) + \left(\frac{2}{10^7}+\frac{3}{10^8}+\frac{7}{10^9}\right) + ...$

2. Define the repeating block: Let $P$ be the sum of the first repeating block of terms: $P = \frac{2}{10}+\frac{3}{10^2}+\frac{7}{10^3}$ To sum these fractions, find a common denominator, which is $10^3 = 1000$: $P = \frac{2 \times 100}{1000}+\frac{3 \times 10}{1000}+\frac{7}{1000} = \frac{200+30+7}{1000} = \frac{237}{1000}$

3. Express the series using the repeating block: Notice how subsequent blocks relate to $P$: The second block is $\frac{2}{10^4}+\frac{3}{10^5}+\frac{7}{10^6} = \frac{1}{10^3}\left(\frac{2}{10}+\frac{3}{10^2}+\frac{7}{10^3}\right) = \frac{1}{10^3}P$. The third block is $\frac{2}{10^7}+\frac{3}{10^8}+\frac{7}{10^9} = \frac{1}{10^6}\left(\frac{2}{10}+\frac{3}{10^2}+\frac{7}{10^3}\right) = \frac{1}{10^6}P$. So the series can be written as: $S = 1 + P + \frac{1}{10^3}P + \frac{1}{10^6}P + ...$ $S = 1 + P \left(1 + \frac{1}{10^3} + \frac{1}{10^6} + ...\right)$

4. Sum the infinite geometric series: The expression in the parenthesis is an infinite geometric series with the first term $a=1$ and common ratio $r=\frac{1}{10^3}$. Since $|r| = \frac{1}{1000} < 1$, the sum of this infinite geometric series is given by the formula $\frac{a}{1-r}$: $\text{Sum of GP} = \frac{1}{1 - \frac{1}{10^3}} = \frac{1}{\frac{1000-1}{1000}} = \frac{1}{\frac{999}{1000}} = \frac{1000}{999}$

5. Substitute and calculate the total sum: Now substitute the values of $P$ and the sum of the geometric series back into the expression for $S$: $S = 1 + \left(\frac{237}{1000}\right) \times \left(\frac{1000}{999}\right)$ The $1000$ in the numerator and denominator cancel out: $S = 1 + \frac{237}{999}$

6. Simplify the fraction: Both 237 and 999 are divisible by 3 (sum of digits $2+3+7=12$ and $9+9+9=27$, both divisible by 3). $237 \div 3 = 79$ $999 \div 3 = 333$ So, $\frac{237}{999} = \frac{79}{333}$.

7. Final Sum: $S = 1 + \frac{79}{333} = \frac{333}{333} + \frac{79}{333} = \frac{333+79}{333} = \frac{412}{333}$

The sum of the infinite series is $\frac{412}{333}$.

The series can also be recognized as a repeating decimal: $1.237237237... = 1.\overline{237}$. To convert this to a fraction: Let $x = 1.\overline{237}$ $x = 1 + 0.\overline{237}$ Let $y = 0.\overline{237}$ $1000y = 237.\overline{237}$ $1000y = 237 + y$ $999y = 237$ $y = \frac{237}{999} = \frac{79}{333}$ So, $x = 1 + \frac{79}{333} = \frac{333+79}{333} = \frac{412}{333}$.