Question
Question: Find the number of solution of the equation in [0, 2π], tan (5π cos α) = cot (5π sin α)...
Find the number of solution of the equation in [0, 2π], tan (5π cos α) = cot (5π sin α)
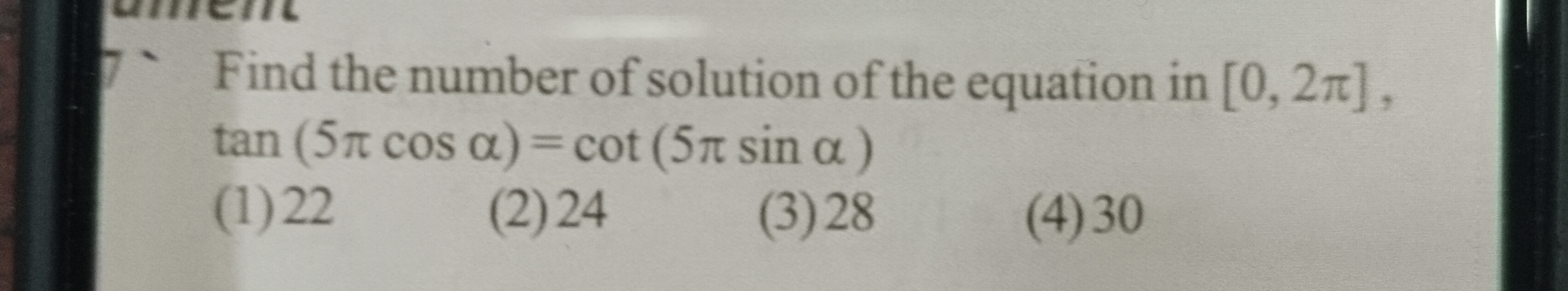
22
24
28
30
28
Solution
The given equation is tan(5πcosα)=cot(5πsinα).
Using the identity cotx=tan(2π−x), we can rewrite the equation as: tan(5πcosα)=tan(2π−5πsinα)
The general solution for tanA=tanB is A=nπ+B, where n is an integer. So, 5πcosα=nπ+(2π−5πsinα).
Dividing the entire equation by π: 5cosα=n+21−5sinα
Rearranging the terms to group cosα and sinα: 5cosα+5sinα=n+21
Divide by 5: cosα+sinα=5n+101=102n+1
We can express the left side, cosα+sinα, in the form Rsin(α+β). Using the R-factorization method, R=12+12=2, and β=4π. So, cosα+sinα=2sin(α+4π).
Substituting this back into the equation: 2sin(α+4π)=102n+1
sin(α+4π)=1022n+1
Let X=α+4π. Since α∈[0,2π], the range for X is [4π,2π+4π]=[4π,49π]. This interval has a length of 2π.
The equation becomes sinX=C, where C=1022n+1. For real solutions to exist, we must have −1≤C≤1. −1≤1022n+1≤1 −102≤2n+1≤102
Since 102≈14.14, the inequality becomes: −14.14≤2n+1≤14.14
Since 2n+1 must be an odd integer, the possible values for 2n+1 are: {−13,−11,−9,−7,−5,−3,−1,1,3,5,7,9,11,13}. This gives a total of 14 possible values for 2n+1.
For each of these 14 values of 2n+1, we get a corresponding value for C. Note that C cannot be 1 or −1 because 2n+1=±102 has no integer solution for n. Also, C cannot be ±21 because 1022n+1=±21⟹2n+1=±10, which has no integer solution for n. Therefore, for each of the 14 values of n, C is strictly between −1 and 1, and C=±21.
For any value of C such that −1<C<1 and C=0, the equation sinX=C has exactly two solutions in any interval of length 2π. Our interval for X is [4π,49π], which has a length of 2π. Since none of the possible values of C are 0, each of the 14 values of n leads to exactly 2 solutions for X in the interval [4π,49π].
This gives a total of 14×2=28 solutions for X.
We must also consider the domain restrictions for the original equation:
- tan(5πcosα) is defined if 5πcosα=2π+kπ, which simplifies to cosα=101+5k for any integer k.
- cot(5πsinα) is defined if 5πsinα=mπ, which simplifies to sinα=5m for any integer m.
It can be shown that for the determined values of n, none of the solutions for α derived from sin(α+4π)=1022n+1 will lead to cosα=101+2k or sinα=5m. Therefore, all 28 solutions are valid.
The number of solutions is 28.
