Solveeit Logo
Login

Question

Question: An element $\overrightarrow{\Delta l}=\Delta x\hat{i}$ is placed at the origin and carries a large c...

An element Δl→=Δxi^\overrightarrow{\Delta l}=\Delta x\hat{i} is placed at the origin and carries a large current I=10AI=10A. The magnetic field on the yy-axis at a distance of 0.5 m from the element Δx\Delta x of 1 cm length is:

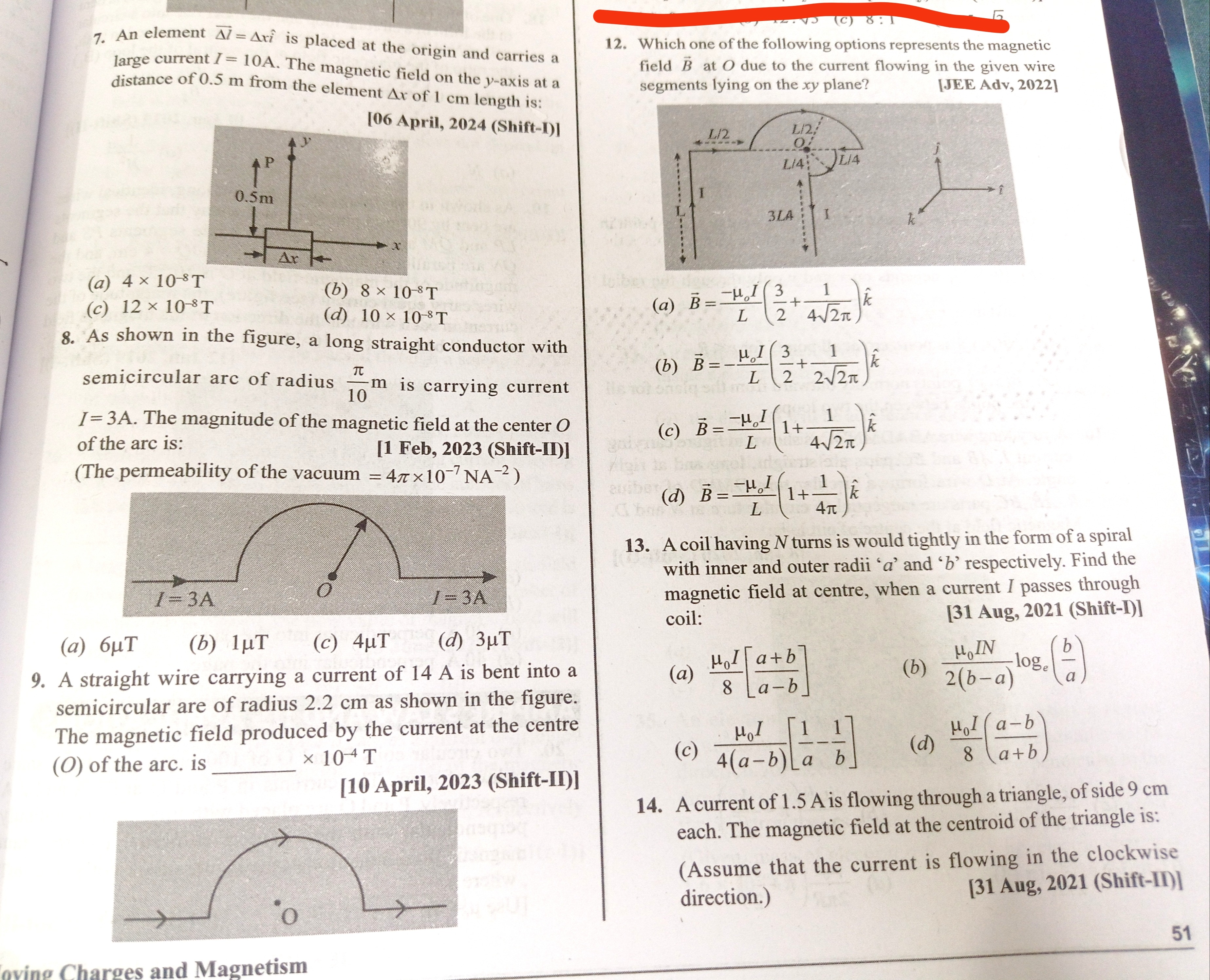
A

4×10−8T4 \times 10^{-8}T

B

8×10−8T8 \times 10^{-8}T

C

12×10−8T12 \times 10^{-8}T

D

10×10−8T10 \times 10^{-8}T

Answer

(a)

Explanation

Solution

The magnetic field dB→\overrightarrow{dB} due to a current element dl→\overrightarrow{dl} at a position vector r⃗\vec{r} from the element is given by the Biot-Savart Law:

dB→=μ04πI(dl→×r⃗)r3\overrightarrow{dB} = \frac{\mu_0}{4\pi} \frac{I (\overrightarrow{dl} \times \vec{r})}{r^3}

Given:

  • I=10 AI = 10 \text{ A}
  • Δx=1 cm=0.01 m\Delta x = 1 \text{ cm} = 0.01 \text{ m}
  • r=0.5 mr = 0.5 \text{ m}
  • μ0=4π×10−7 Tm/A\mu_0 = 4\pi \times 10^{-7} \text{ Tm/A}

The magnitude of the magnetic field is:

B=μ04πIΔxr2=10−710×0.010.52=10−70.10.25=4×10−8 TB = \frac{\mu_0}{4\pi} \frac{I \Delta x}{r^2} = 10^{-7} \frac{10 \times 0.01}{0.5^2} = 10^{-7} \frac{0.1}{0.25} = 4 \times 10^{-8} \text{ T}