Question
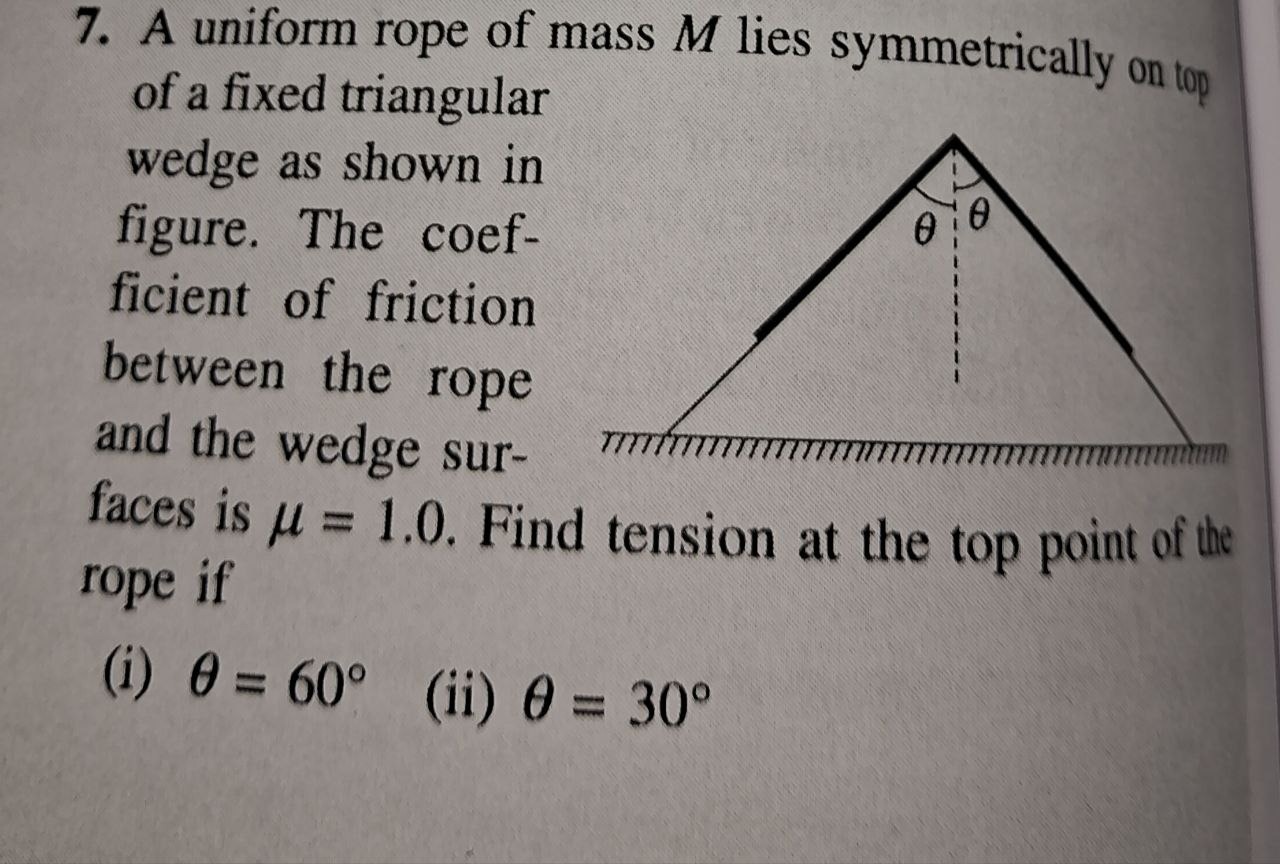
Question: A uniform rope of mass $M$ lies symmetrically on top of a fixed triangular wedge as shown in figure....
A uniform rope of mass M lies symmetrically on top of a fixed triangular wedge as shown in figure. The coefficient of friction between the rope and the wedge surfaces is μ=1.0. Find tension at the top point of the rope if
(i) θ=60∘ (ii) θ=30∘
(i) Ttop=4Mg(3−1) (ii) Ttop=0
Solution
The tension at the top of the rope depends on whether the rope has a natural tendency to slide down the wedge.
-
If tanθ>μ, the gravitational force component along the incline is greater than the maximum possible static friction. The rope would slide if not held. The tension at the top provides the necessary force to prevent sliding, and friction acts maximally upwards. The tension is Ttop=2Mg(sinθ−μcosθ).
-
If tanθ≤μ, the gravitational force component along the incline is less than or equal to the maximum possible static friction. The rope is stable on its own; friction alone can prevent it from sliding. Thus, no tension is required at the top to hold it, so Ttop=0.
Applying these conditions:
(i) For θ=60∘, tan60∘=3≈1.732. Since μ=1.0, tan60∘>μ. So, Ttop=2Mg(sin60∘−1⋅cos60∘)=2Mg(23−21)=4Mg(3−1).
(ii) For θ=30∘, tan30∘=31≈0.577. Since μ=1.0, tan30∘<μ. So, Ttop=0.
