Question

A stationary wave is represented by $y = 12 \cos(\frac{\pi}{6}x) \sin(8\pi t)$, where x and y are in cm and t in second. The distance between two successive antinodes is

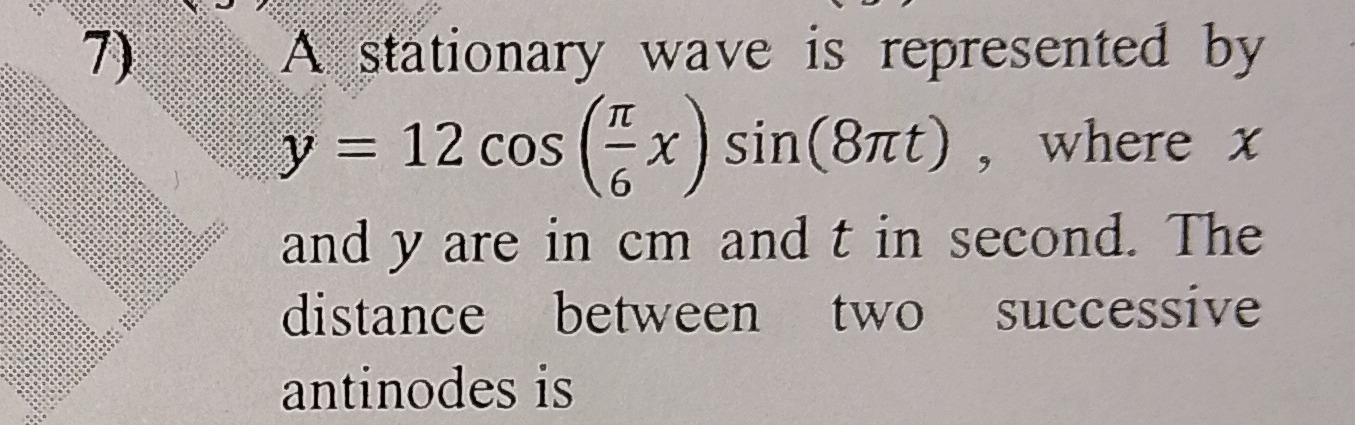
• A. 3 cm
• B. 6 cm
• C. 12 cm
• D. 24 cm

Answer 1

Answer: (B)

6 cm

Answer 2

The given stationary wave is

$$y = 12 \cos\left(\frac{\pi}{6}x\right)\sin(8\pi t).$$

This is of the form

$$y = A\cos(kx)\sin(\omega t)$$

with the wave number

$$k = \frac{\pi}{6}.$$

For a standing wave of this form, the antinodes occur at positions where the amplitude factor $\cos\left(kx\right)$ is maximum, i.e., where

$$\cos\left(kx\right) = \pm1.$$

This happens when

$$\frac{\pi}{6}x = m\pi \quad \Rightarrow \quad x = 6m \quad (m \text{ integer}).$$

Thus, the distance between two successive antinodes is

$$\Delta x = x_{m+1} - x_m = 6 \text{ cm}.$$