Question
Question: A particle moving in the positive x direction has initial velocity $v_0$. The particle undergoes ret...
A particle moving in the positive x direction has initial velocity v0. The particle undergoes retardation kv2, where v is instantaneous velocity. The velocity of the particle as a function of time is
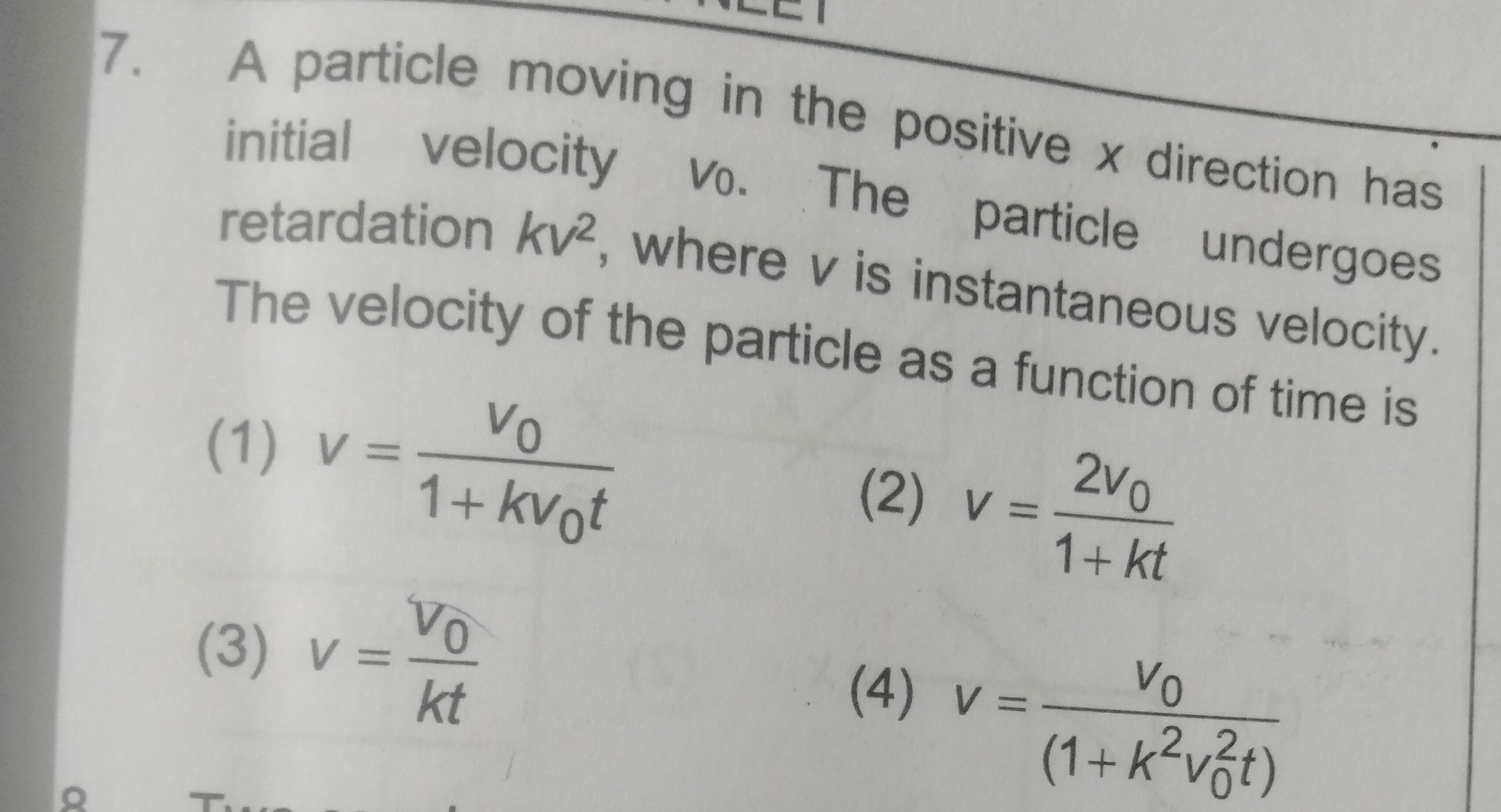
v=1+kv0tv0
v=1+kt2v0
v=ktv0
v=(1+k2v02t)v0
(1) v=1+kv0tv0
Solution
The problem describes the motion of a particle undergoing retardation (deceleration) proportional to the square of its instantaneous velocity. We need to find the velocity as a function of time.
-
Define acceleration:
Retardation means the acceleration is negative. Given retardation is kv2, the acceleration a is:
a=dtdv=−kv2 -
Separate variables:
To solve this differential equation, separate the variables v and t:
v2dv=−kdt -
Integrate both sides:
Integrate the left side with respect to v from the initial velocity v0 (at t=0) to the instantaneous velocity v (at time t). Integrate the right side with respect to t from 0 to t.
∫v0vv2dv=∫0t−kdt -
Perform integration:
The integral of 1/v2 is −1/v.
[−v1]v0v=−k[t]0t
(−v1)−(−v01)=−k(t−0)
−v1+v01=−kt -
Rearrange to solve for v:
v01−v1=−kt
v1=v01+kt
To combine the terms on the right, find a common denominator:
v1=v01+kv0t
Now, invert both sides to get v:
v=1+kv0tv0
This expression gives the velocity of the particle as a function of time.
