Question

A hollow conducting sphere of inner radius R and outer radius 2R is given a charge Q as shown in the figure, then the

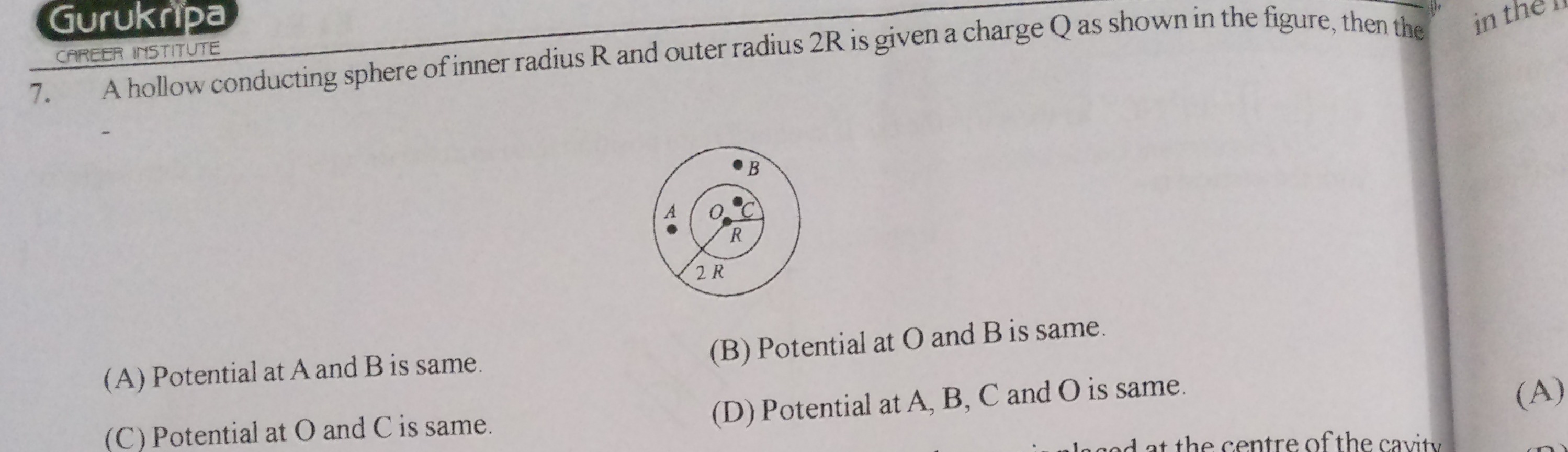
• A. Potential at A and B is same.
• B. Potential at O and B is same.
• C. Potential at O and C is same.
• D. Potential at A, B, C and O is same.

Answer 1

Answer: (C)

C

Answer 2

The hollow conducting sphere has inner radius R and outer radius 2R. A charge Q is given to the sphere.
In electrostatic equilibrium, the electric field inside a conductor is zero. Also, any net charge resides on the surface(s) of the conductor.
Since there is no charge in the cavity, there is no induced charge on the inner surface (at radius R). The entire charge Q resides on the outer surface (at radius 2R).

Let's find the electric potential at different points.
For a point outside the sphere at a distance $r > 2R$, the potential is the same as that of a point charge Q at the center:
$V(r) = \frac{1}{4\pi\epsilon_0} \frac{Q}{r}$ for $r > 2R$.

Inside the conductor (R < r < 2R), the electric field is zero. Since $E = -\frac{dV}{dr} = 0$, the potential is constant inside the conductor. This constant potential is equal to the potential on the outer surface, which is at $r=2R$.
$V(r) = V(2R) = \frac{1}{4\pi\epsilon_0} \frac{Q}{2R}$ for $R \le r \le 2R$.

Inside the cavity (r < R), the electric field is zero because there is no charge inside the cavity and no charge on the inner surface. Since $E = -\frac{dV}{dr} = 0$, the potential is constant inside the cavity. This constant potential is equal to the potential on the inner surface, which is at $r=R$.
$V(r) = V(R) = \frac{1}{4\pi\epsilon_0} \frac{Q}{2R}$ for $0 \le r < R$.

So, the potential at any point within the cavity or within the conductor (including the surfaces) is constant and equal to $\frac{Q}{4\pi\epsilon_0 (2R)}$.
Points O (center, r=0), C (inside cavity, r<R), and A (inside conductor, R<r<2R) are all in the region where the potential is constant.
$V_O = \frac{Q}{4\pi\epsilon_0 (2R)}$
$V_C = \frac{Q}{4\pi\epsilon_0 (2R)}$
$V_A = \frac{Q}{4\pi\epsilon_0 (2R)}$

Point B is outside the conductor at a distance $r_B > 2R$.
$V_B = \frac{Q}{4\pi\epsilon_0 r_B}$.

Comparing the potentials:
$V_O = V_C = V_A$.
Since $r_B > 2R$, we have $\frac{1}{r_B} < \frac{1}{2R}$, so $V_B < V_A$ (assuming Q is positive).

Thus, the potential at O and C is the same.