Question
Question: A bob of heavy mass $m$ is suspended by a light string of length $l$. The bob is given a horizontal ...
A bob of heavy mass m is suspended by a light string of length l. The bob is given a horizontal velocity v0 as shown in figure. If the string gets slack at some point P making an angle θ from the horizontal, the ratio of the speed v of the bob at point P to its initial speed v0 is:
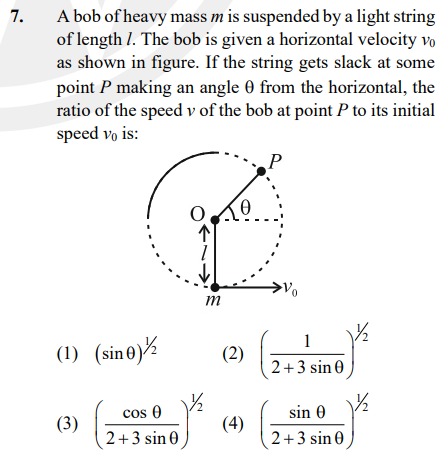
(sinθ)21
(2+3sinθ1)21
(2+3sinθcosθ)21
(2+3sinθsinθ)21
(2+3sinθsinθ)21
Solution
Here's the step-by-step explanation:
-
Apply conservation of mechanical energy between the lowest point and point P where the string gets slack.
-
Define the height of point P relative to the lowest point using the angle θ. The height is h=l(1+sinθ).
-
Write the energy conservation equation: 21mv02=21mv2+mgl(1+sinθ).
-
At point P, the string gets slack, meaning the tension is zero. Apply Newton's second law in the radial direction. The component of gravity along the string towards the center is mgsinθ. This provides the centripetal force: mgsinθ=lmv2.
-
From the tension equation, find v2=glsinθ.
-
Substitute the expression for v2 into the energy conservation equation to find v02.
-
Calculate the ratio v/v0 by taking the square root of the ratio of v2 and v02.
Therefore, v0v=(2+3sinθsinθ)21.
