Question
Question: The interval in which $y = x^2e^{2x}$ is increasing is...
The interval in which y=x2e2x is increasing is
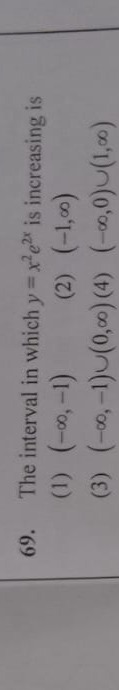
(−∞,−1)
(−1,∞)
(−∞,−1)∪(0,∞)
(−∞,0)∪(1,∞)
(−∞,−1)∪(0,∞)
Solution
To determine the interval where the function y=x2e2x is increasing, we need to find its first derivative, dxdy, and analyze its sign.
-
Find the first derivative: We use the product rule, (uv)′=u′v+uv′, where u=x2 and v=e2x. u′=dxd(x2)=2x v′=dxd(e2x)=e2x⋅dxd(2x)=2e2x
So, dxdy=(2x)(e2x)+(x2)(2e2x) dxdy=2xe2x+2x2e2x Factor out the common terms, 2xe2x: dxdy=2xe2x(1+x)
-
Find critical points: Set dxdy=0 to find the critical points: 2xe2x(1+x)=0 Since e2x is always positive for all real x, we only need to consider the other factors: 2x(1+x)=0 This equation yields two critical points: 2x=0⇒x=0 1+x=0⇒x=−1
-
Analyze the sign of dxdy: The critical points x=−1 and x=0 divide the real number line into three intervals: (−∞,−1), (−1,0), and (0,∞). We test the sign of dxdy in each interval. Remember that the sign of dxdy is determined by the sign of 2x(1+x) since e2x>0.
-
Interval (−∞,−1): Choose a test value, e.g., x=−2. 2(−2)(1+(−2))=−4(−1)=4. Since 4>0, dxdy>0 in this interval. Thus, y is increasing.
-
Interval (−1,0): Choose a test value, e.g., x=−0.5. 2(−0.5)(1+(−0.5))=−1(0.5)=−0.5. Since −0.5<0, dxdy<0 in this interval. Thus, y is decreasing.
-
Interval (0,∞): Choose a test value, e.g., x=1. 2(1)(1+1)=2(2)=4. Since 4>0, dxdy>0 in this interval. Thus, y is increasing.
-
-
Conclusion: The function y=x2e2x is increasing when dxdy>0. This occurs in the intervals (−∞,−1) and (0,∞). The union of these intervals is (−∞,−1)∪(0,∞).
