Question
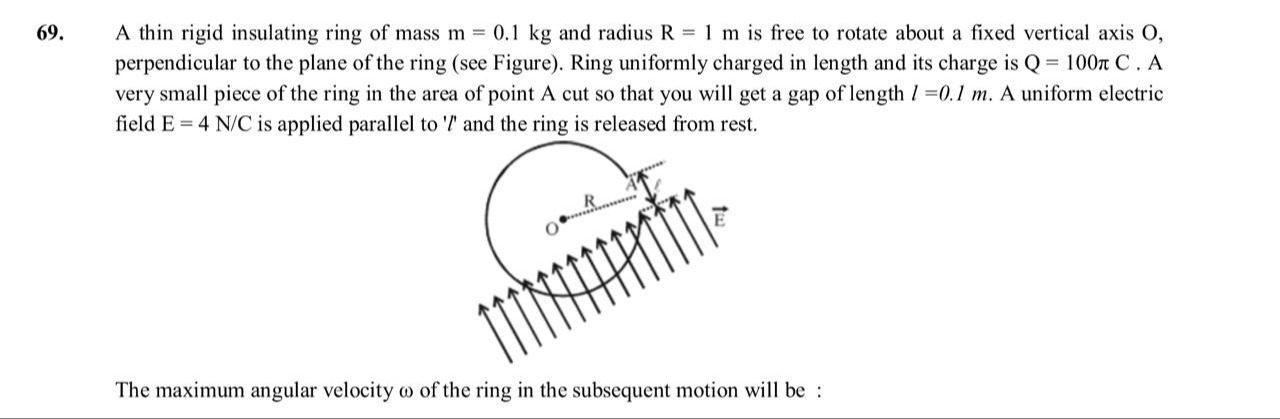
Question: 69. A thin rigid insulating ring of mass m = 0.1 kg and radius R = 1 m is free to rotate about a fix...
- A thin rigid insulating ring of mass m = 0.1 kg and radius R = 1 m is free to rotate about a fixed vertical axis O, perpendicular to the plane of the ring (see Figure). Ring uniformly charged in length and its charge is Q = 100π C. A very small piece of the ring in the area of point A cut so that you will get a gap of length l =0.1 m. A uniform electric field E = 4 N/C is applied parallel to 'l' and the ring is released from rest.
The maximum angular velocity ω of the ring in the subsequent motion will be :
20\sqrt{2} rad/s
Solution
Solution:
-
Find the missing charge and effective dipole moment:
- Charge per unit length on the ring: λ=2πRQ
- Charge missing due to the gap of length l: Δq=λl=2πRQl
- This missing charge at a distance R creates an effective dipole moment: p=Δq⋅R=2πQl.
-
Energy considerations:
ΔU=U(π)−U(0)=[pE]−[−pE]=2pE.
When the ring rotates, the change in electric potential energy of the dipole in the field E is converted into rotational kinetic energy. The potential energy of a dipole in an electric field is U=−pEcosθ. If the dipole rotates from an initially unstable (anti-parallel) position (θ=π) to the stable (parallel) alignment (θ=0), the change in potential energy is: -
Relate potential energy change to rotational kinetic energy:
21Iω2,
The rotational kinetic energy is given by:where for a thin ring I=mR2. Equate the energy change to the kinetic energy:
21mR2ω2=2pE.Solving for ω:
ω=mR24pE. -
Substitute p=2πQl into the expression:
ω=mR24(2πQl)E=πmR22QlE. -
Plug in the given values:
ω=π⋅0.1⋅122⋅100π⋅0.1⋅4=0.1π80π=800.
Q=100πC,l=0.1m,E=4N/C,m=0.1kg,R=1m:Thus,
ω=202rad/s.
Explanation (Minimal):
- Compute missing charge: Δq=2πRQl.
- Effective dipole moment: p=Δq⋅R=2πQl.
- Change in potential energy: ΔU=2pE.
- Equate 21mR2ω2=2pE and solve for ω.
- Substitute given values to get ω=202 rad/s.
Answer:
202 rad/sSubject, Chapter, and Topic:
- Subject: Physics
- Chapter: Electrostatics & Rotational Motion (from NCERT Class 12; topics include Electric Charges and Fields, and Dynamics of Rotational Motion)
- Topic: Electric Dipoles in a Uniform Electric Field and Energy Conservation in Rotational Motion
