Question

$\int \frac{(1-cos2x)}{(1+cos2x)}dx=?$

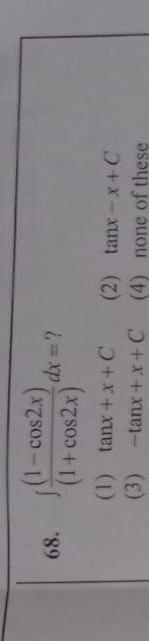
• A. tanx+x+C
• B. tanx-x+C
• C. -tanx+x+C
• D. none of these

Answer 1

Answer: (B)

tanx-x+C

Answer 2

To solve the integral $\int \frac{(1-\cos2x)}{(1+\cos2x)}dx$, we use standard trigonometric identities.

1. Use half-angle identities:
   We know the following trigonometric identities:

   • $1 - \cos2x = 2\sin^2x$
   • $1 + \cos2x = 2\cos^2x$

2. Substitute these identities into the integral: $\int \frac{(1-\cos2x)}{(1+\cos2x)}dx = \int \frac{2\sin^2x}{2\cos^2x}dx$

3. Simplify the expression: $\int \frac{\sin^2x}{\cos^2x}dx = \int \tan^2x dx$

4. Use the Pythagorean identity for $\tan^2x$:
   We know that $\sec^2x - \tan^2x = 1$, which implies $\tan^2x = \sec^2x - 1$.

5. Substitute this identity into the integral: $\int \tan^2x dx = \int (\sec^2x - 1)dx$

6. Integrate term by term: $\int (\sec^2x - 1)dx = \int \sec^2x dx - \int 1 dx$

7. Perform the integration:
   We know that:

   • $\int \sec^2x dx = \tan x + C_1$
   • $\int 1 dx = x + C_2$

   Combining these, we get: $\tan x - x + C$ where $C$ is the constant of integration ($C = C_1 - C_2$).

Therefore, the final answer is $\tan x - x + C$.