Question

$\sqrt{\frac{\mu_0}{\epsilon_0}}$ A red LED emits light of 0.1 watt uniformly around it. The amplitude of the electric field of the light distance of 1 $m$ from the diode is:

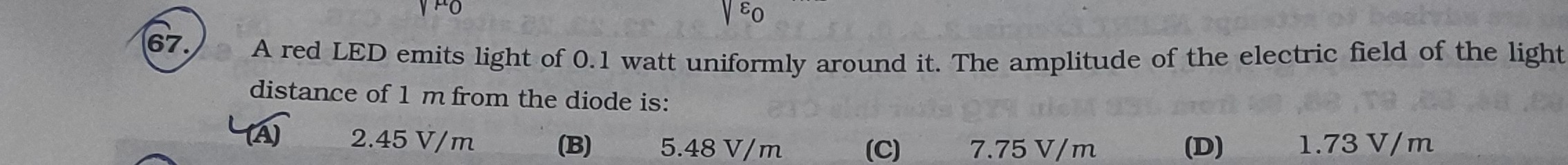
• A. 2.45 V/m
• B. 5.48 V/m
• C. 7.75 V/m
• D. 1.73 V/m

Answer 1

Answer: (A)

2.45 V/m

Answer 2

The light emitted by the LED can be considered as a point source radiating uniformly in all directions.

The intensity ($I$) of light at a distance $r$ from a source with power $P$ is given by: $I = \frac{P}{4\pi r^2}$

For an electromagnetic wave, the intensity is also related to the amplitude of the electric field ($E_0$) by the formula: $I = \frac{1}{2} \epsilon_0 c E_0^2$ where $\epsilon_0$ is the permittivity of free space ($8.854 \times 10^{-12} \, \text{F/m}$) and $c$ is the speed of light in vacuum ($3 \times 10^8 \, \text{m/s}$).

Equating the two expressions for intensity: $\frac{P}{4\pi r^2} = \frac{1}{2} \epsilon_0 c E_0^2$

Now, we solve for $E_0^2$: $E_0^2 = \frac{2P}{4\pi r^2 \epsilon_0 c} = \frac{P}{2\pi \epsilon_0 c r^2}$

We know that $\frac{1}{4\pi \epsilon_0} = k$, where $k$ is Coulomb's constant, approximately $9 \times 10^9 \, \text{N m}^2/\text{C}^2$. So, we can rewrite the expression for $E_0^2$ as: $E_0^2 = \frac{2P}{c r^2} \times \frac{1}{4\pi \epsilon_0} = \frac{2Pk}{c r^2}$

Given values: Power, $P = 0.1 \, \text{watt}$ Distance, $r = 1 \, \text{m}$ Speed of light, $c = 3 \times 10^8 \, \text{m/s}$ Coulomb's constant, $k = 9 \times 10^9 \, \text{N m}^2/\text{C}^2$

Substitute these values into the equation for $E_0^2$: $E_0^2 = \frac{2 \times 0.1 \times (9 \times 10^9)}{(3 \times 10^8) \times (1)^2}$ $E_0^2 = \frac{1.8 \times 10^9}{3 \times 10^8}$ $E_0^2 = 0.6 \times 10^{(9-8)}$ $E_0^2 = 0.6 \times 10^1$ $E_0^2 = 6$

Now, take the square root to find $E_0$: $E_0 = \sqrt{6} \, \text{V/m}$ $E_0 \approx 2.449 \, \text{V/m}$

Rounding to two decimal places, $E_0 \approx 2.45 \, \text{V/m}$.

The initial expression $\sqrt{\frac{\mu_0}{\epsilon_0}}$ represents the impedance of free space, $Z_0$. The intensity can also be expressed as $I = \frac{E_0^2}{2Z_0}$. Since $Z_0 = \frac{1}{\epsilon_0 c}$, this leads to the same formula $I = \frac{1}{2}\epsilon_0 c E_0^2$.