Question

A motor boat is going in a river with a velocity $\overrightarrow{V}=(4\hat{i}-2\hat{j}+\hat{k})ms^{-1}$. If the force due to motor is $\overrightarrow{F}=(5\hat{i}-10\hat{j}+6\hat{k})N$, then the power of the motor boat is:

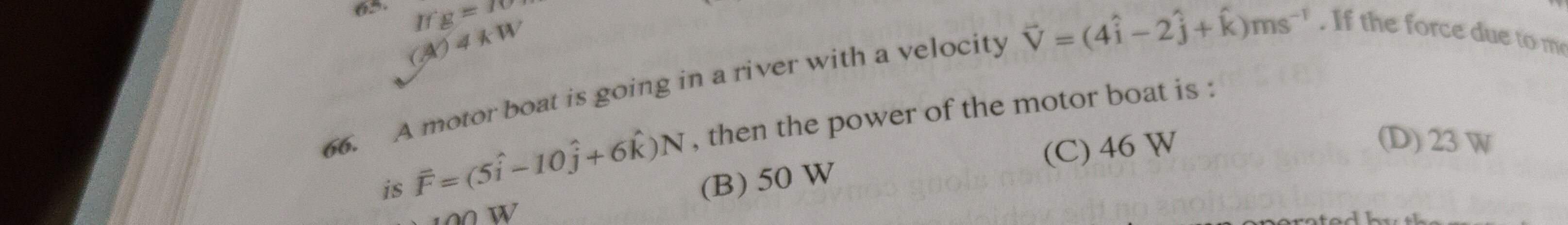
• A. 100 W
• B. 50 W
• C. 46 W
• D. 23 W

Answer 1

Answer: (C)

46 W

Answer 2

The power of a motor boat is given by the dot product of the force applied by the motor and the velocity of the boat. The formula for power $P$ is:

$P = \vec{F} \cdot \vec{V}$

Given:

Velocity of the boat, $\overrightarrow{V}=(4\hat{i}-2\hat{j}+\hat{k}) \, ms^{-1}$

Force due to the motor, $\overrightarrow{F}=(5\hat{i}-10\hat{j}+6\hat{k}) \, N$

Substitute the given vectors into the power formula:

$P = (5\hat{i}-10\hat{j}+6\hat{k}) \cdot (4\hat{i}-2\hat{j}+\hat{k})$

To calculate the dot product, multiply the corresponding components and sum them up:

$P = (5)(4) + (-10)(-2) + (6)(1)$

$P = 20 + 20 + 6$

$P = 46 \, W$

Thus, the power of the motor boat is 46 W.