Solveeit Logo
Login

Question

Question: If $A + B = \begin{bmatrix} 1 & \tan \frac{\theta}{2} \\ -\tan \frac{\theta}{2} & 1 \end{bmatrix}$ w...

If A+B=[1tan⁡θ2−tan⁡θ21]A + B = \begin{bmatrix} 1 & \tan \frac{\theta}{2} \\ -\tan \frac{\theta}{2} & 1 \end{bmatrix} where AA is symmetric and BB is skew-symmetric matrix, then the matrix (A−1B+AB−1)(A^{-1}B + AB^{-1}) at θ=π6\theta = \frac{\pi}{6} is given by

A

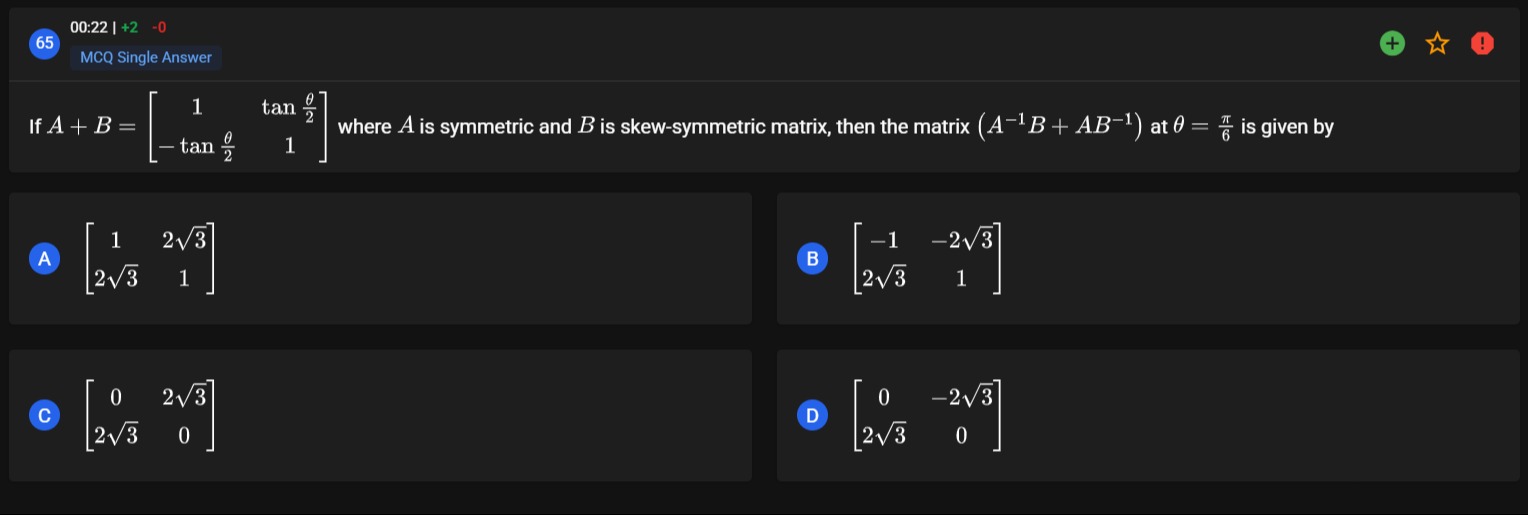
[123231]\begin{bmatrix} 1 & 2\sqrt{3} \\ 2\sqrt{3} & 1 \end{bmatrix}

B

[−1−23231]\begin{bmatrix} -1 & -2\sqrt{3} \\ 2\sqrt{3} & 1 \end{bmatrix}

C

[023230]\begin{bmatrix} 0 & 2\sqrt{3} \\ 2\sqrt{3} & 0 \end{bmatrix}

D

[0−23230]\begin{bmatrix} 0 & -2\sqrt{3} \\ 2\sqrt{3} & 0 \end{bmatrix}

Answer

[0−23230]\begin{bmatrix} 0 & -2\sqrt{3} \\ 2\sqrt{3} & 0 \end{bmatrix}

Explanation

Solution

Here's how to solve the problem:

  1. Decompose the matrix: Express AA and BB in terms of the given matrix and its transpose. Since AA is symmetric and BB is skew-symmetric, we have:

    A=12(M+MT)A = \frac{1}{2}(M + M^T) and B=12(M−MT)B = \frac{1}{2}(M - M^T), where M=[1tan⁡(θ2)−tan⁡(θ2)1]M = \begin{bmatrix} 1 & \tan(\frac{\theta}{2}) \\ -\tan(\frac{\theta}{2}) & 1 \end{bmatrix}.

  2. Calculate A and B: Compute AA and BB using the formulas above. You'll find that A=IA = I (the identity matrix) and B=[0tan⁡(θ2)−tan⁡(θ2)0]B = \begin{bmatrix} 0 & \tan(\frac{\theta}{2}) \\ -\tan(\frac{\theta}{2}) & 0 \end{bmatrix}.

  3. Simplify the expression: Since A=IA = I, the expression A−1B+AB−1A^{-1}B + AB^{-1} simplifies to B+B−1B + B^{-1}.

  4. Calculate B inverse: Find the inverse of BB. If t=tan⁡(θ2)t = \tan(\frac{\theta}{2}), then B=[0t−t0]B = \begin{bmatrix} 0 & t \\ -t & 0 \end{bmatrix}, and B−1=[0−1t1t0]B^{-1} = \begin{bmatrix} 0 & -\frac{1}{t} \\ \frac{1}{t} & 0 \end{bmatrix}.

  5. Compute B + B inverse: Add BB and B−1B^{-1}: B+B−1=[0t−1t−t+1t0]B + B^{-1} = \begin{bmatrix} 0 & t - \frac{1}{t} \\ -t + \frac{1}{t} & 0 \end{bmatrix}.

  6. Evaluate at theta = pi/6: Substitute θ=π6\theta = \frac{\pi}{6}. Then t=tan⁡(π12)=2−3t = \tan(\frac{\pi}{12}) = 2 - \sqrt{3}. Also, 1t=2+3\frac{1}{t} = 2 + \sqrt{3}.

  7. Final Calculation: Calculate t−1t=(2−3)−(2+3)=−23t - \frac{1}{t} = (2 - \sqrt{3}) - (2 + \sqrt{3}) = -2\sqrt{3}. Therefore, B+B−1=[0−23230]B + B^{-1} = \begin{bmatrix} 0 & -2\sqrt{3} \\ 2\sqrt{3} & 0 \end{bmatrix}.

Thus, the final answer is [0−23230]\begin{bmatrix} 0 & -2\sqrt{3} \\ 2\sqrt{3} & 0 \end{bmatrix}.