Solveeit Logo
Login

Question

Question: The cartesian coordinates of the point on the parabola \(y^2 = -16x\), with, whose parameter is \(\f...

The cartesian coordinates of the point on the parabola y2=−16xy^2 = -16x, with, whose parameter is 12\frac{1}{2}, are

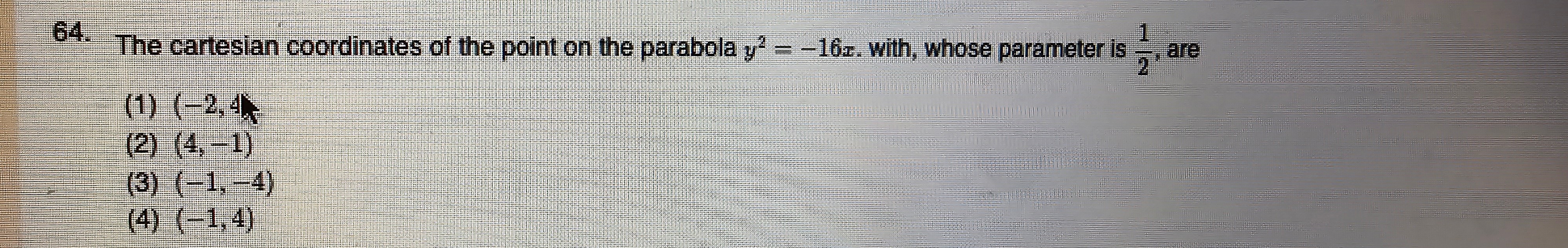
A

(-2,4)

B

(4,-1)

C

(-1,-4)

D

(-1,4)

Answer

Option (3): (−1,−4)(-1, -4).

Explanation

Solution

For the parabola y2=−16xy^2 = -16x, rewriting it in the form y2=4axy^2 = 4ax gives:

4a=−16  ⟹  a=−4.4a = -16 \implies a = -4.

The parametric equations for a parabola are:

x=at2,y=2at.x = at^2, \quad y = 2at.

For parameter t=12t = \frac{1}{2}:

x=−4(12)2=−4(14)=−1,y=2(−4)(12)=−4.x = -4\left(\frac{1}{2}\right)^2 = -4\left(\frac{1}{4}\right) = -1, \quad y = 2(-4)\left(\frac{1}{2}\right) = -4.