Question

If $x^2 + y^2 = t + \frac{1}{t}$ and $x^4 + y^4 = t^2 + \frac{1}{t^2}$,

$\frac{dy}{dx}$ is equal to

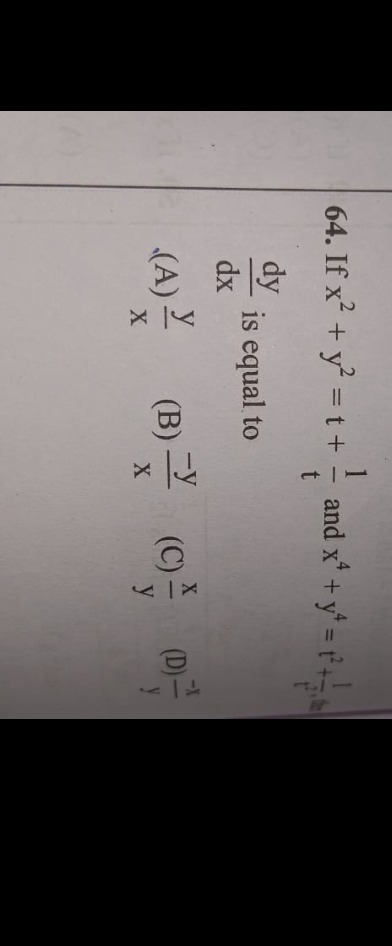
• A. $\frac{y}{x}$
• B. $\frac{-y}{x}$
• C. $\frac{x}{y}$
• D. $\frac{-x}{y}$

Answer 1

Answer: (B)

$\frac{-y}{x}$

Answer 2

We are given:

$$x^2 + y^2 = t + \frac{1}{t} \quad \text{(1)}$$ $$x^4 + y^4 = t^2 + \frac{1}{t^2} \quad \text{(2)}$$

Step 1: Eliminate $t$ using the identity

Square equation (1):

$$(x^2 + y^2)^2 = \left(t + \frac{1}{t}\right)^2 = t^2 + 2 + \frac{1}{t^2}$$

But we also know from (1) and (2) that:

$$(x^2 + y^2)^2 = x^4 + y^4 + 2x^2y^2 = \left(t^2+\frac{1}{t^2}\right) + 2x^2y^2$$

Equate the two expressions:

$$t^2 + 2 + \frac{1}{t^2} = t^2 + \frac{1}{t^2} + 2x^2y^2$$

This simplifies to:

$$2 = 2x^2y^2 \quad \Longrightarrow \quad x^2y^2 = 1$$

Step 2: Differentiate the relation

Differentiate $x^2y^2 = 1$ with respect to $x$:

$$\frac{d}{dx}(x^2y^2) = 0$$

Using the product and chain rules:

$$2x\,y^2 + 2x^2y\,\frac{dy}{dx} = 0$$

Divide by $2xy$ (assuming $x \neq 0$ and $y \neq 0$):

$$\frac{x\,y^2}{xy} + \frac{x^2y}{xy}\frac{dy}{dx} = 0 \quad \Longrightarrow \quad y + x\frac{dy}{dx} = 0$$

Thus:

$$\frac{dy}{dx} = -\frac{y}{x}$$