Question
Question: If $\lim_{x\to 0} \frac{\sin x \sin 2x \sin 3x...\sin nx - x^n}{x \tan((1+x)(1+2x)(1+3x)....(1+2023x...
If limx→0xtan((1+x)(1+2x)(1+3x)....(1+2023x))sinxsin2xsin3x...sinnx−xn exists and is non-zero, then 'n' equals
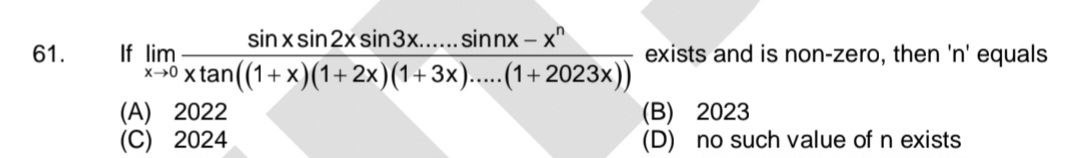
2022
2023
2024
no such value of n exists
no such value of n exists
Solution
Let the limit be L. The numerator is N(x)=∏k=1nsinkx−xn and the denominator is D(x)=xtan(∏k=12023(1+kx)).
For the denominator, as x→0, ∏k=12023(1+kx)→1. Thus, tan(∏k=12023(1+kx))→tan(1). The denominator behaves as D(x)∼xtan(1) for x→0. The lowest power of x is x1.
For the numerator, using the Taylor expansion siny=y−6y3+O(y5): ∏k=1nsinkx=∏k=1n(kx−6(kx)3+O(x5)) =(x−6x3+...)(2x−6(2x)3+...)...(nx−6(nx)3+...) The term with the lowest power of x in the product is (x)(2x)...(nx)=n!xn. So, ∏k=1nsinkx=n!xn+O(xn+2).
The numerator is N(x)=n!xn+O(xn+2)−xn=(n!−1)xn+O(xn+2).
For the limit L to exist and be non-zero, the lowest power of x in the numerator must match the lowest power of x in the denominator, which is x1.
Case 1: n>1. The lowest power of x in the numerator is xn. For this to match the denominator's x1, we need n=1. This contradicts the assumption n>1.
Case 2: n=1. The numerator is N(x)=sinx−x. Using Taylor expansion, sinx−x=(x−6x3+O(x5))−x=−6x3+O(x5). The lowest power of x in the numerator is x3. The denominator's lowest power is x1. The limit becomes L=limx→0xtan(1)−x3/6=limx→06tan(1)−x2=0. This limit is zero, not non-zero.
Since neither n=1 nor n>1 yields a non-zero limit, there is no such value of n that satisfies the given condition.
