Question
Question: A current carrying wire AC is placed in uniform transverse magnetic field then the force on wire AC ...
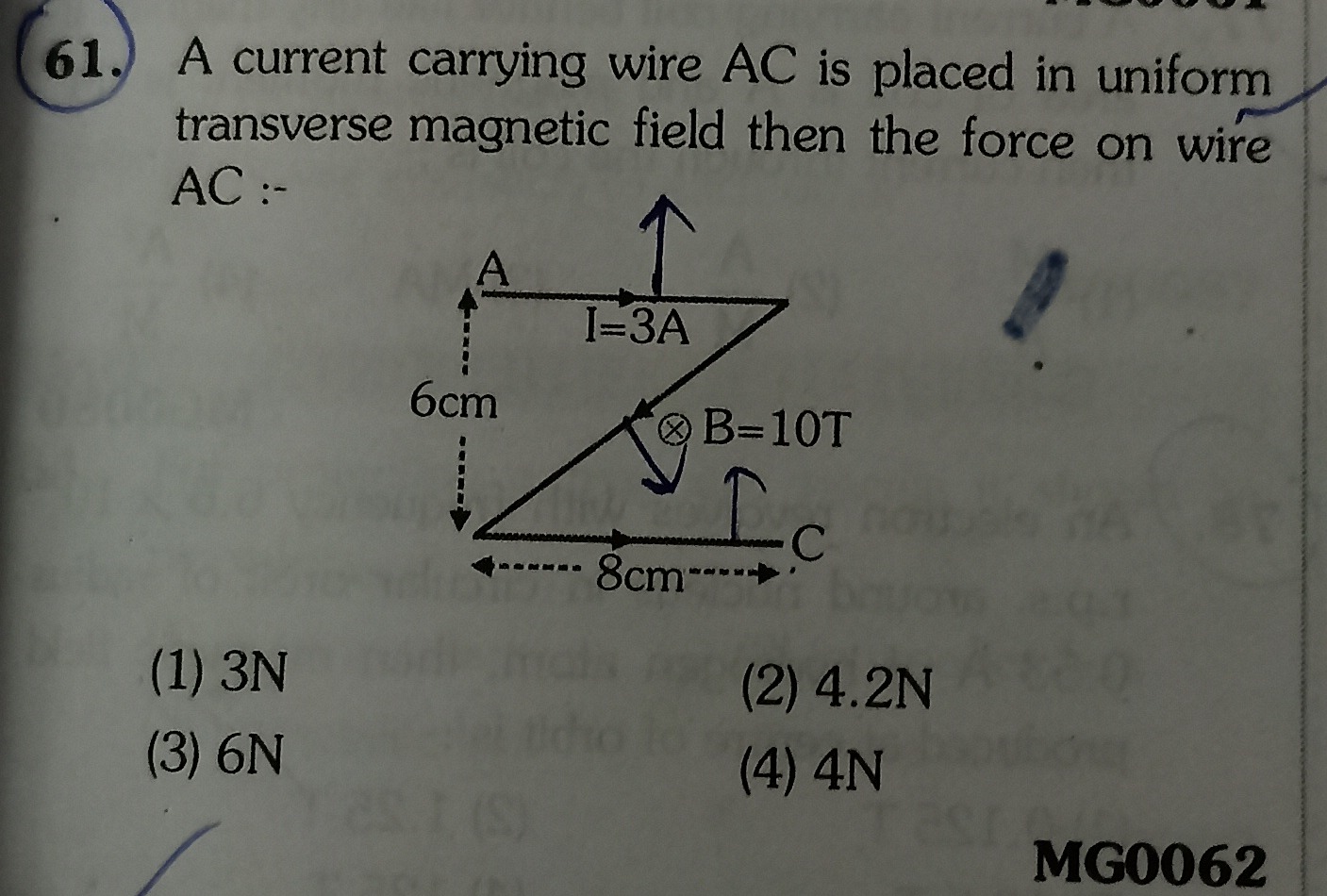
A current carrying wire AC is placed in uniform transverse magnetic field then the force on wire AC :-
3N
4.2N
6N
4N
3N
Solution
The problem asks for the force on a current-carrying wire AC placed in a uniform transverse magnetic field.
Key Concept:
For a current-carrying wire of any shape placed in a uniform magnetic field, the net magnetic force on the wire depends only on the current (I), the magnetic field strength (B), and the displacement vector (L) from the initial point to the final point of the wire. The formula for the force is:
F=I(L×B)
where L is the displacement vector from point A to point C.
Step-by-step Derivations:
-
Identify the displacement vector LAC:
From the given figure, the wire starts at point A and ends at point C. The vertical distance between the horizontal line passing through A and the horizontal line passing through C is 6 cm. This means the y-component of the displacement is -6 cm (since C is below A). The horizontal distance between the vertical line passing through A and the vertical line passing through C is 8 cm. This means the x-component of the displacement is +8 cm (since C is to the right of A). So, the displacement vector is LAC=(8i^−6j^) cm.
-
Convert dimensions to SI units:
Lx=8 cm=0.08 m Ly=−6 cm=−0.06 m So, LAC=(0.08i^−0.06j^) m.
-
Calculate the magnitude of the effective length (Leff):
Leff=∣LAC∣=(0.08 m)2+(−0.06 m)2 Leff=0.0064+0.0036 Leff=0.01 Leff=0.1 m
-
Identify the given values:
Current I=3 A Magnetic field B=10 T The magnetic field is "transverse" and indicated by ⊗, which means it is uniform and directed into the page. This implies the magnetic field is perpendicular to the plane containing the wire (and thus perpendicular to the displacement vector LAC). Therefore, the angle (θ) between LAC and B is 90∘.
-
Calculate the magnitude of the force:
Since LAC and B are perpendicular, the magnitude of the force is given by: F=ILeffBsinθ F=ILeffBsin(90∘) F=ILeffB Substitute the values: F=(3 A)×(0.1 m)×(10 T) F=3×1 N F=3 N
The force on the wire AC is 3 N.
Explanation of the solution:
The force on a current-carrying wire in a uniform magnetic field is given by F=I(L×B), where L is the displacement vector from the start to the end of the wire. From the diagram, the displacement from A to C is 8 cm horizontally and 6 cm vertically downwards. The magnitude of this effective length is (8 cm)2+(6 cm)2=10 cm=0.1 m. Since the magnetic field is uniform and perpendicular to the plane of the wire, the angle between L and B is 90∘. Therefore, the magnitude of the force is F=ILB=(3 A)×(0.1 m)×(10 T)=3 N.
