Question

The value of $\lambda$ such that the system $x - 2y + z = -4, 2x - y + 2z = 2$ and $x + y + \lambda z = 4$ has no solution is

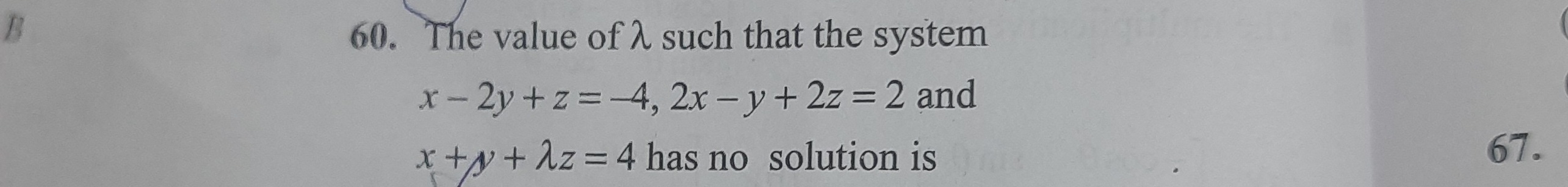
• A. 3
• B. 1
• C. 0
• D. -3

Answer 1

Answer: (B)

1

Answer 2

Given the system

$$\begin{aligned} x - 2y + z &= -4 \quad (1),\\[5mm] 2x - y + 2z &= 2 \quad (2),\\[5mm] x + y + \lambda z &= 4 \quad (3). \end{aligned}$$

1. Find the determinant of the coefficient matrix:

$$A = \begin{vmatrix} 1 & -2 & 1\\[4mm] 2 & -1 & 2\\[4mm] 1 & 1 & \lambda \end{vmatrix}.$$

Expanding the determinant:

$$\begin{aligned} \det(A) &= 1\begin{vmatrix} -1 & 2 \\[3mm] 1 & \lambda \end{vmatrix} - (-2) \begin{vmatrix} 2 & 2 \\[3mm] 1 & \lambda \end{vmatrix} + 1\begin{vmatrix} 2 & -1 \\[3mm] 1 & 1 \end{vmatrix}\\[3mm] &= 1\bigl[(-1)\lambda - (2)(1)\bigr] + 2\bigl[2\lambda - 2\cdot1\bigr] + 1\bigl[2\cdot1 - (-1)\cdot1\bigr]\\[3mm] &= (-\lambda - 2) + 2(2\lambda-2) + (2+1)\\[3mm] &= -\lambda - 2 + 4\lambda - 4 + 3\\[3mm] &= 3\lambda - 3 = 3(\lambda-1). \end{aligned}$$

For the system to possibly be inconsistent (i.e. not have a unique solution), we require $\det(A)=0$, hence

$$3(\lambda-1)=0 \quad \Longrightarrow \quad \lambda=1.$$

2. Check for consistency when $\lambda=1$:

Substitute $\lambda=1$ into the equations:

$$\begin{aligned} (1)&\quad x - 2y + z = -4,\\[3mm] (2)&\quad 2x - y + 2z = 2,\\[3mm] (3)&\quad x + y + z = 4. \end{aligned}$$

• From (1): $x = -4 + 2y - z$.

• Substitute $x$ into (2):

  $$2(-4+2y-z) - y + 2z = 2 \quad\Longrightarrow\quad -8 + 4y - 2z - y + 2z = 2,$$

  which simplifies to

  $$3y - 8 = 2 \quad\Longrightarrow\quad 3y=10 \quad\Longrightarrow\quad y=\frac{10}{3}.$$

• Then, $x = -4 + \frac{20}{3} - z = \frac{8}{3} - z$.

• Substitute $x$ and $y$ into (3):

  $$\left(\frac{8}{3}-z\right)+\frac{10}{3}+z = 4 \quad\Longrightarrow\quad \frac{18}{3}=6=4.$$

This contradiction shows that the system is inconsistent when $\lambda=1$.