Question
Question: If $a^2x^4+b^2y^4=c^6$, then maximum value of $xy$ is...
If a2x4+b2y4=c6, then maximum value of xy is
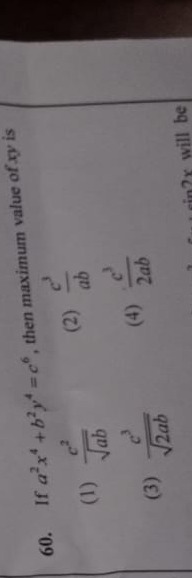
abc2
abc3
2abc3
2abc3
2abc3
Solution
To find the maximum value of xy given the equation a2x4+b2y4=c6, we can use the AM-GM inequality.
1. Apply AM-GM Inequality: The AM-GM inequality states that for two non-negative numbers A and B, their arithmetic mean is greater than or equal to their geometric mean: 2A+B≥AB Equality holds when A=B.
Let A=a2x4 and B=b2y4. Since x4 and y4 are always non-negative, and a2,b2 are also non-negative, A and B are non-negative. Substitute A and B into the AM-GM inequality: 2a2x4+b2y4≥a2x4⋅b2y4 We are given a2x4+b2y4=c6. Substitute this into the left side: 2c6≥a2b2x4y4 Simplify the right side: 2c6≥(ab)2(x2y2)2 2c6≥∣abx2y2∣ Since x2y2 is non-negative, and for the maximum value of xy to be positive, we assume ab>0. Thus, ∣abx2y2∣=abx2y2. 2c6≥abx2y2 Rearrange the inequality to find the upper bound for x2y2: x2y2≤2abc6 To maximize xy, we need to maximize x2y2. The maximum value of x2y2 is 2abc6.
2. Find the maximum value of xy: Take the square root of the maximum value of x2y2: xy=2abc6 xy=2abc6 xy=2abc3
3. Condition for Maximum Value: The maximum value occurs when the equality in the AM-GM inequality holds, which means A=B: a2x4=b2y4 Substitute this condition back into the original equation a2x4+b2y4=c6: a2x4+a2x4=c6 2a2x4=c6⟹x4=2a2c6 Similarly, b2y4+b2y4=c6 2b2y4=c6⟹y4=2b2c6 Now, calculate x2y2: x2=2a2c6=2ac3 y2=2b2c6=2bc3 (We take the positive square roots since x2 and y2 are non-negative.) Then, x2y2=(2ac3)(2bc3)=2abc6 Finally, xy=2abc6=2abc3.
This confirms the maximum value derived from the AM-GM inequality.
