Question
Question: Value of: $Tan 20 \cdot Cot 50 \cdot Tan 80 = ?$...
Value of:
Tan20⋅Cot50⋅Tan80=?
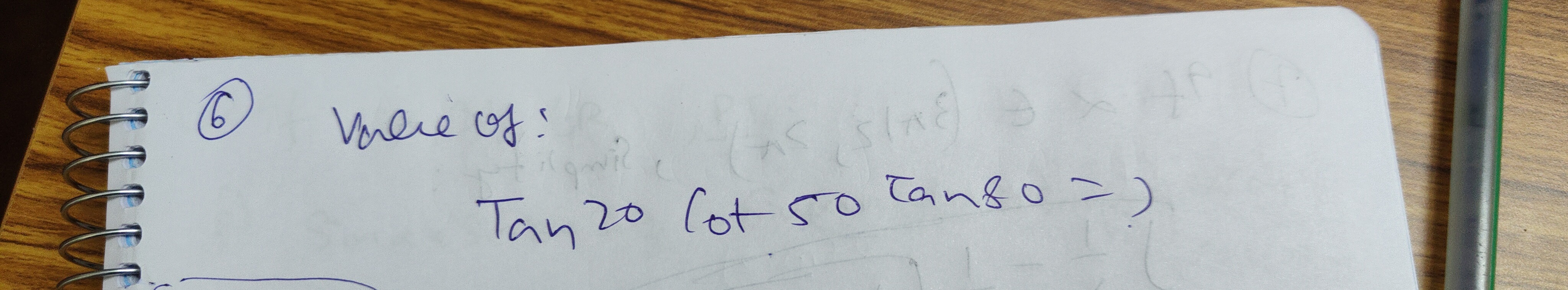
3
Solution
To find the value of the expression Tan20∘⋅Cot50∘⋅Tan80∘, we will use trigonometric identities.
Step 1: Convert Cot50∘ to an equivalent Tan form. We know that Cotθ=Tan(90∘−θ). So, Cot50∘=Tan(90∘−50∘)=Tan40∘.
Step 2: Substitute the converted term back into the expression. The expression becomes: Tan20∘⋅Tan40∘⋅Tan80∘
Step 3: Recognize the pattern. This expression fits the general trigonometric identity: Tanθ⋅Tan(60∘−θ)⋅Tan(60∘+θ)=Tan(3θ)
In our expression, if we let θ=20∘:
- The first term is Tan20∘.
- The second term is Tan40∘=Tan(60∘−20∘).
- The third term is Tan80∘=Tan(60∘+20∘).
Thus, the expression exactly matches the pattern with θ=20∘.
Step 4: Apply the identity. Using the identity, the value of the expression is Tan(3⋅θ). Substitute θ=20∘: Tan(3⋅20∘)=Tan60∘
Step 5: Recall the standard value of Tan60∘. We know that Tan60∘=3.
Therefore, the value of the given expression is 3.
