Question

6. The value(s) of x satisfying $1-\log_{9}(x+1)^{2}=\tfrac{1}{2}\log_{\sqrt{3}}\bigl(\tfrac{x+5}{x+3}\bigr)$ is/are:

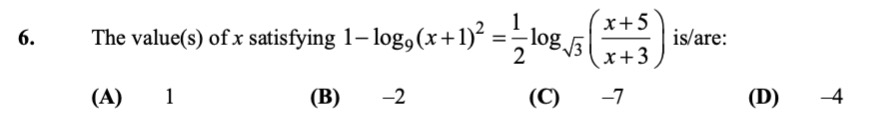
• A. 1
• B. -2
• C. -7
• D. -4

Answer 1

Answer: (A)

1

Answer 2

Step 1. Rewrite in base 3:

$$\log_{9}(x+1)^{2}=\frac{\log_{3}(x+1)^{2}}{\log_{3}9} =\frac{2\log_{3}(x+1)}{2} =\log_{3}(x+1),$$ $$\log_{\sqrt{3}}\bigl(\tfrac{x+5}{x+3}\bigr) =\frac{\log_{3}\bigl(\tfrac{x+5}{x+3}\bigr)}{\log_{3}\sqrt{3}} =\frac{\log_{3}\bigl(\tfrac{x+5}{x+3}\bigr)}{\tfrac12} =2\log_{3}\bigl(\tfrac{x+5}{x+3}\bigr).$$

Thus the equation becomes

$$1-\log_{3}(x+1) =\tfrac12\cdot2\log_{3}\Bigl(\tfrac{x+5}{x+3}\Bigr) =\log_{3}\Bigl(\tfrac{x+5}{x+3}\Bigr).$$

Step 2. Convert 1 to $\log_{3}3$:

$$\log_{3}3-\log_{3}(x+1) =\log_{3}\!\Bigl(\tfrac{3}{x+1}\Bigr) =\log_{3}\!\Bigl(\tfrac{x+5}{x+3}\Bigr).$$

Hence

$$\frac{3}{x+1}=\frac{x+5}{x+3} \;\Longrightarrow\; 3(x+3)=(x+5)(x+1) \;\Longrightarrow\; x^{2}+3x-4=0 \;\Longrightarrow\; x=1\text{ or }x=-4.$$

Step 3. Check domains:

• $x+1>0\implies x>-1$.
• $\tfrac{x+5}{x+3}>0$. Only $x=1$ satisfies both. Therefore the solution is $x=1$.