Question
Question: The value of $\lim_{n \to \infty} \frac{1+2-3+4+5-6+.......+(3n-2)+(3n-1)-3n}{\sqrt{2n^4+4n+3}-\sqrt...
The value of limn→∞2n4+4n+3−n4+5n+41+2−3+4+5−6+.......+(3n−2)+(3n−1)−3n is:
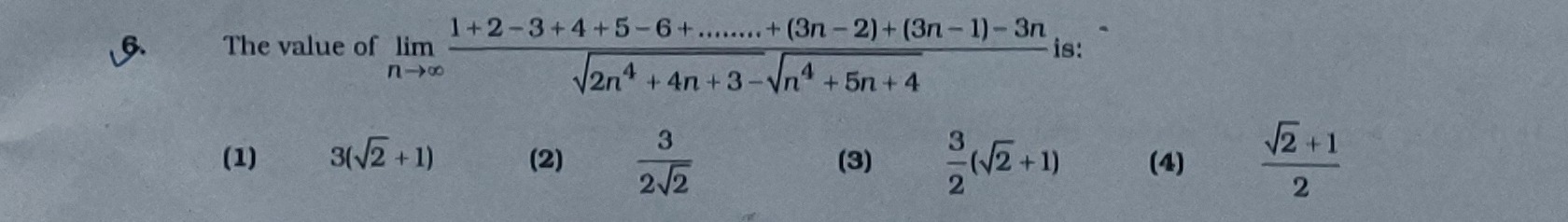
A
3(2+1)
B
223
C
23(2+1)
D
22+1
Answer
23(2+1)
Explanation
Solution
The numerator series can be grouped as (1+2−3)+(4+5−6)+⋯+((3n−2)+(3n−1)−3n). Each group sums to 0,3,6,…,3n−3. The sum of these n terms is an arithmetic progression: 2n(0+3n−3)=23n(n−1).
The denominator is Dn=2n4+4n+3−n4+5n+4. Rationalizing the denominator gives: Dn=2n4+4n+3+n4+5n+4(2n4+4n+3)−(n4+5n+4)=2n4+4n+3+n4+5n+4n4−n−1.
For large n, the dominant terms are: Numerator ∼23n2. Denominator ∼2n4+n4n4=2n2+n2n4=(2+1)n2n4=2+1n2.
The limit is: limn→∞2+1n223n2=23(2+1)
