Question

The phase difference between two particles in a medium separated by a distance x is $\pi/6$. If the frequency of the oscillation is 50 Hz and the velocity of propagation of the wave is 100 m/s, then x =

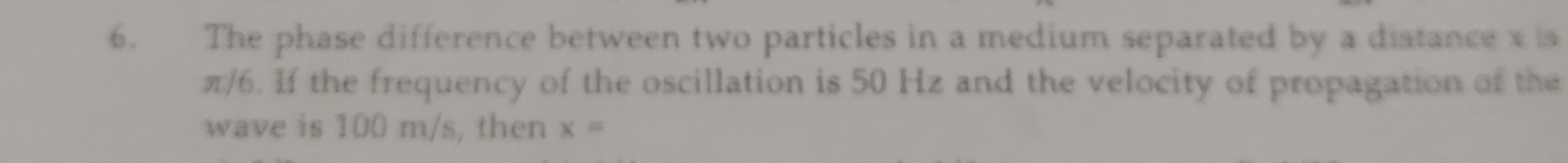
Answer 1

x = 1/6 m

Answer 2

1. Find the wavelength (λ):

   $$\lambda = \frac{v}{f} = \frac{100}{50} = 2 \, \text{m}$$

2. Relate phase difference (φ) to distance (x):

   For a wave,

   $$\phi = \frac{2\pi}{\lambda} \, x$$

   Given $\phi = \frac{\pi}{6}$, substituting:

   $$\frac{\pi}{6} = \frac{2\pi}{2} \, x \quad \Rightarrow \quad \frac{\pi}{6} = \pi \, x$$

   Solving for $x$:

   $$x = \frac{1}{6} \, \text{m}$$

Minimal Explanation:

Wavelength $\lambda = 2$ m. Phase relation: $\frac{\pi}{6} = \pi x$ yields $x = \frac{1}{6}$ m.