Question
Question: The number of integral value of x satisfying the equation $|\log_{\sqrt{3}}x-2|-|\log_3x-2|=2$, is...
The number of integral value of x satisfying the equation ∣log3x−2∣−∣log3x−2∣=2, is
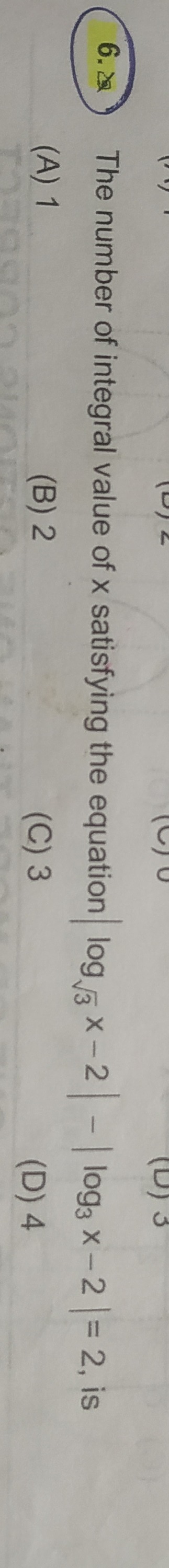
1
2
3
4
1
Solution
Here's how to solve the equation ∣log3x−2∣−∣log3x−2∣=2:
-
Simplify the Logarithms: Recognize that log3x=2log3x. This allows us to rewrite the equation as ∣2log3x−2∣−∣log3x−2∣=2.
-
Substitution: Let y=log3x. The equation becomes 2∣y−1∣−∣y−2∣=2.
-
Solve the Absolute Value Equation: Consider three cases:
-
Case 1: y<1. Then 2(1−y)−(2−y)=2, which simplifies to −y=2, so y=−2.
-
Case 2: 1≤y<2. Then 2(y−1)−(2−y)=2, which simplifies to 3y−4=2, so y=2. However, this solution is not strictly less than 2, so it's not valid in this interval.
-
Case 3: y≥2. Then 2(y−1)−(y−2)=2, which simplifies to y=2.
-
-
Substitute Back: We found y=−2 and y=2. Substituting back y=log3x:
-
If log3x=−2, then x=3−2=91.
-
If log3x=2, then x=32=9.
-
-
Identify Integral Solutions: Of the two solutions x=91 and x=9, only x=9 is an integer.
Therefore, there is only 1 integral value of x that satisfies the equation.
