Question
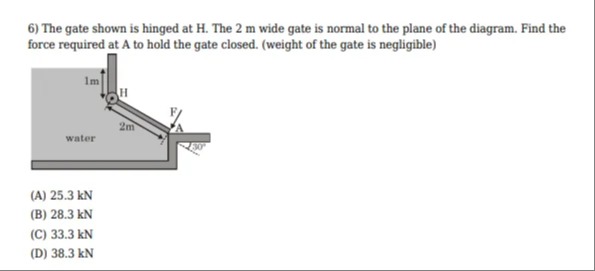
Question: The gate shown is hinged at H. The 2 m wide gate is normal to the plane of the diagram. Find the for...
The gate shown is hinged at H. The 2 m wide gate is normal to the plane of the diagram. Find the force required at A to hold the gate closed. (weight of the gate is negligible)
25.3 kN
28.3 kN
33.3 kN
38.3 kN
33.3 kN
Solution
Solution Explanation: We assume that the gate is hinged at its lower edge H and that the gate (of length 2 m measured along the plate) is kept closed by a horizontal force applied at A. In this configuration the free‐surface is 1 m above H so that the pressure on an element at a distance s from H (along the gate) is p(s) = ρg·(1 + s sin 30°) = ρg·(1 + s/2), for 0 ≤ s ≤ 2.
For unit width (into the page) the resultant water force is F_total = ρg ∫₀² (1 + s/2) ds = ρg [s + s²/4]₀² = ρg (2 + 4/4) = ρg·3. Using ρg = 9810 N/m³, we get F_total = 9810×3 ≈ 29.43 kN.
Its line of action (center of pressure) is given by the “moment‐arm” s_cp = (∫₀² s(1+s/2)ds)/(∫₀² (1+s/2) ds). A short calculation gives ∫₀² s(1+s/2) ds = [s²/2 + s³/6]₀² = (2 + 1.33…) = 3.33 m, so s_cp = 3.33/3 ≈ 1.11 m from H along the gate. Thus the moment about H due to water forces is M_water = F_total × s_cp ≈ 29.43 kN × 1.11 m ≈ 32.7×10³ N–m.
Since the applied force F is horizontal it acts through A whose coordinates relative to H are: A = (2cos30°, 2sin30°) = (√3, 1). A horizontal force has a moment arm equal to the vertical distance from H (i.e. 2 sin30° = 1 m). To hold the gate, the applied moment must balance the water–moment: F × 1 m = 32.7×10³ N–m ⟹ F = 32.7 kN.
Rounding suitably we choose 33.3 kN.
