Solveeit Logo
Login

Question

Question: The exact value of $\frac{60 \sin 82^{\circ} \sin 51^{\circ} \sin 47^{\circ}}{\sin 16^{\circ} + \sin...

The exact value of 60sin⁡82∘sin⁡51∘sin⁡47∘sin⁡16∘+sin⁡78∘+sin⁡86∘\frac{60 \sin 82^{\circ} \sin 51^{\circ} \sin 47^{\circ}}{\sin 16^{\circ} + \sin 78^{\circ} + \sin 86^{\circ}} is -

A

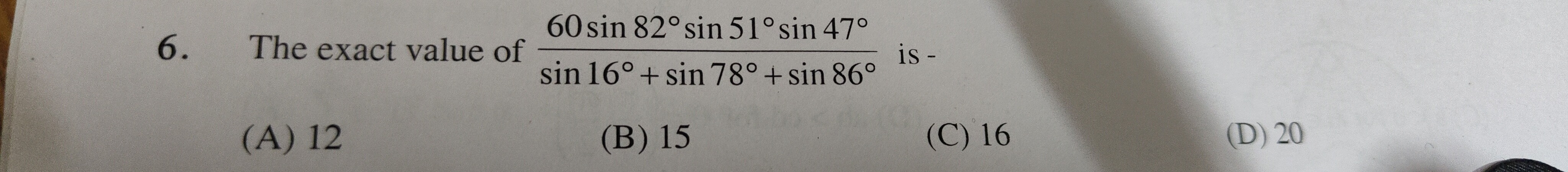
12

B

15

C

16

D

20

Answer

15

Explanation

Solution

The problem asks for the exact value of the trigonometric expression 60sin⁡82∘sin⁡51∘sin⁡47∘sin⁡16∘+sin⁡78∘+sin⁡86∘\frac{60 \sin 82^{\circ} \sin 51^{\circ} \sin 47^{\circ}}{\sin 16^{\circ} + \sin 78^{\circ} + \sin 86^{\circ}}.

Let's analyze the numerator and the denominator separately.

1. Analyze the Numerator:

The numerator is N=60sin⁡82∘sin⁡51∘sin⁡47∘N = 60 \sin 82^{\circ} \sin 51^{\circ} \sin 47^{\circ}. We can use the complementary angle identity: sin⁡x=cos⁡(90∘−x)\sin x = \cos(90^{\circ} - x). Applying this identity to each term in the numerator: sin⁡82∘=cos⁡(90∘−82∘)=cos⁡8∘\sin 82^{\circ} = \cos(90^{\circ} - 82^{\circ}) = \cos 8^{\circ}

sin⁡51∘=cos⁡(90∘−51∘)=cos⁡39∘\sin 51^{\circ} = \cos(90^{\circ} - 51^{\circ}) = \cos 39^{\circ}

sin⁡47∘=cos⁡(90∘−47∘)=cos⁡43∘\sin 47^{\circ} = \cos(90^{\circ} - 47^{\circ}) = \cos 43^{\circ}

Substituting these into the numerator, we get: N=60cos⁡8∘cos⁡39∘cos⁡43∘N = 60 \cos 8^{\circ} \cos 39^{\circ} \cos 43^{\circ}

2. Analyze the Denominator:

The denominator is D=sin⁡16∘+sin⁡78∘+sin⁡86∘D = \sin 16^{\circ} + \sin 78^{\circ} + \sin 86^{\circ}. First, let's check the sum of the angles in the denominator: 16∘+78∘+86∘=180∘16^{\circ} + 78^{\circ} + 86^{\circ} = 180^{\circ}. This is a key observation. When the sum of three angles A,B,CA, B, C is 180∘180^{\circ} (i.e., A+B+C=180∘A+B+C = 180^{\circ}), a useful trigonometric identity for the sum of their sines is: sin⁡A+sin⁡B+sin⁡C=4cos⁡(A2)cos⁡(B2)cos⁡(C2)\sin A + \sin B + \sin C = 4 \cos\left(\frac{A}{2}\right) \cos\left(\frac{B}{2}\right) \cos\left(\frac{C}{2}\right) Applying this identity to the denominator with A=16∘A=16^{\circ}, B=78∘B=78^{\circ}, and C=86∘C=86^{\circ}: The half-angles are: A2=16∘2=8∘\frac{A}{2} = \frac{16^{\circ}}{2} = 8^{\circ}

B2=78∘2=39∘\frac{B}{2} = \frac{78^{\circ}}{2} = 39^{\circ}

C2=86∘2=43∘\frac{C}{2} = \frac{86^{\circ}}{2} = 43^{\circ}

So, the denominator becomes: D=4cos⁡8∘cos⁡39∘cos⁡43∘D = 4 \cos 8^{\circ} \cos 39^{\circ} \cos 43^{\circ}

3. Compute the Ratio:

Now, substitute the simplified expressions for the numerator and the denominator back into the original expression: 60sin⁡82∘sin⁡51∘sin⁡47∘sin⁡16∘+sin⁡78∘+sin⁡86∘=60cos⁡8∘cos⁡39∘cos⁡43∘4cos⁡8∘cos⁡39∘cos⁡43∘\frac{60 \sin 82^{\circ} \sin 51^{\circ} \sin 47^{\circ}}{\sin 16^{\circ} + \sin 78^{\circ} + \sin 86^{\circ}} = \frac{60 \cos 8^{\circ} \cos 39^{\circ} \cos 43^{\circ}}{4 \cos 8^{\circ} \cos 39^{\circ} \cos 43^{\circ}} Since 8∘,39∘,43∘8^{\circ}, 39^{\circ}, 43^{\circ} are acute angles, cos⁡8∘\cos 8^{\circ}, cos⁡39∘\cos 39^{\circ}, and cos⁡43∘\cos 43^{\circ} are all non-zero. Therefore, we can cancel the common terms cos⁡8∘cos⁡39∘cos⁡43∘\cos 8^{\circ} \cos 39^{\circ} \cos 43^{\circ} from both the numerator and the denominator: =604= \frac{60}{4} =15= 15

The exact value of the given expression is 15.