Question

6. The circle $x^2 + y^2 - 2x - 3ky - 2 = 0$ passes through two fixed points

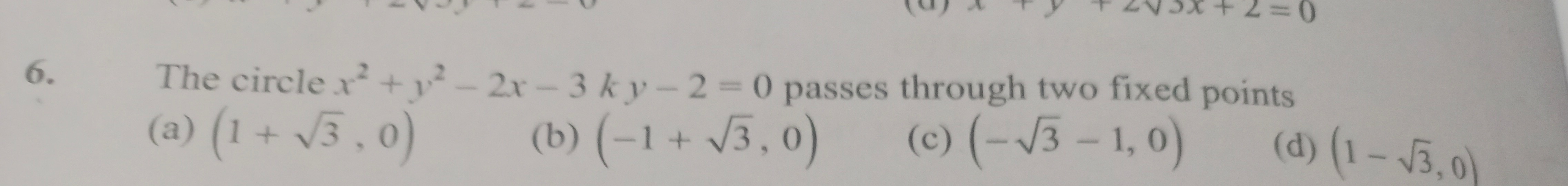
• A. $(1 + \sqrt{3}, 0)$
• B. $(-1 + \sqrt{3}, 0)$
• C. $(-\sqrt{3} - 1, 0)$
• D. $(1 - \sqrt{3}, 0)$

Answer 1

Answer: (A), (D)

$(1 + \sqrt{3}, 0)$ and $(1 - \sqrt{3}, 0)$

Answer 2

1. For the circle

   $$x^2+y^2-2x-3ky-2=0,$$

   to pass through a fixed point $(x_0,y_0)$ for all $k$, the term containing $k$ must vanish when we substitute the point. This gives

   $$-3k\,y_0=0 \quad \Rightarrow \quad y_0 = 0.$$

2. With $y=0$, the equation becomes

   $$x^2 - 2x - 2=0.$$

3. Solving for $x$:

   $$x = \frac{2 \pm \sqrt{4 + 8}}{2} = \frac{2 \pm \sqrt{12}}{2} = \frac{2 \pm 2\sqrt{3}}{2} = 1 \pm \sqrt{3}.$$

Thus, the fixed points are $\left(1+\sqrt{3}, 0\right)$ and $\left(1-\sqrt{3}, 0\right)$.