Question

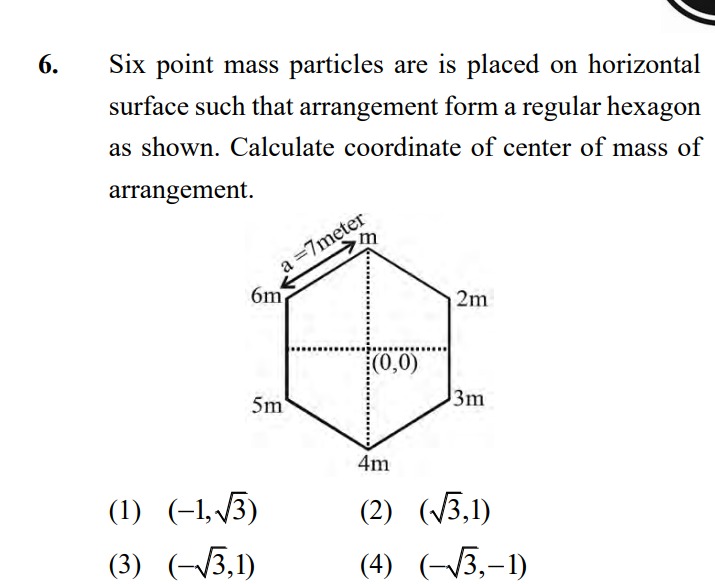
Six point mass particles are placed on horizontal surface such that arrangement form a regular hexagon as shown. Calculate coordinate of center of mass of arrangement.

• A. (-1,$\sqrt{3}$)
• B. ($\sqrt{3}$,1)
• C. (-$\sqrt{3}$,1)
• D. (-$\sqrt{3}$,-1)

Answer 1

Answer: (D)

(-\sqrt{3},-1)

Answer 2

The center of mass $X_{CM}$ and $Y_{CM}$ are calculated using the formulas: $X_{CM} = \frac{\sum m_i x_i}{\sum m_i}$ and $Y_{CM} = \frac{\sum m_i y_i}{\sum m_i}$. Assuming the hexagon is centered at the origin and the side length is $R=7$. The masses and their coordinates are:

1. $m$ at $(0, R)$
2. $2m$ at $(\frac{\sqrt{3}}{2}R, \frac{1}{2}R)$
3. $3m$ at $(\frac{\sqrt{3}}{2}R, -\frac{1}{2}R)$
4. $4m$ at $(0, -R)$
5. $5m$ at $(-\frac{\sqrt{3}}{2}R, -\frac{1}{2}R)$
6. $6m$ at $(-\frac{\sqrt{3}}{2}R, \frac{1}{2}R)$

Total mass $M = 21m$.

$\sum m_i x_i = m(0) + 2m(\frac{\sqrt{3}}{2}R) + 3m(\frac{\sqrt{3}}{2}R) + 4m(0) + 5m(-\frac{\sqrt{3}}{2}R) + 6m(-\frac{\sqrt{3}}{2}R) = -3mR\sqrt{3}$. $\sum m_i y_i = m(R) + 2m(\frac{1}{2}R) + 3m(-\frac{1}{2}R) + 4m(-R) + 5m(-\frac{1}{2}R) + 6m(\frac{1}{2}R) = -3mR$.

Substituting $R=7$: $X_{CM} = \frac{-3m(7)\sqrt{3}}{21m} = -\sqrt{3}$. $Y_{CM} = \frac{-3m(7)}{21m} = -1$. The center of mass is $(-\sqrt{3}, -1)$.