Question

6 $\log_a x. \log_{10} a. \log_a 5$

• 3$^{\log_{10}(x/10)}$ = 9$^{\log_{100} x + \log_4 2}$

or x: - $\frac{5}{6}$

Answer 1

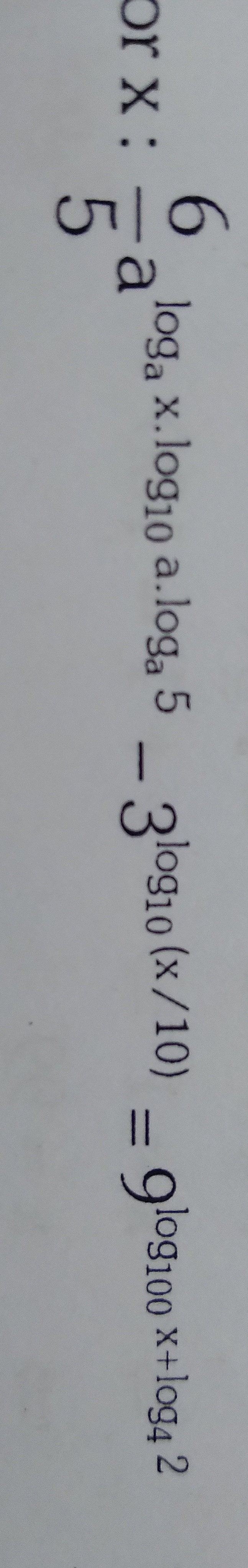
The equation as stated has no real solution.

Answer 2

The given equation is $\log_a x. \log_{10} a. \log_a 5 - 3^{\log_{10}(x/10)} = 9^{\log_{100} x + \log_4 2}$.

Assuming $a=5$ for simplification, the first term becomes $\log_{10} x \cdot \log_a 5 = \log_{10} x \cdot \log_5 5 = \log_{10} x$.

The second term is $- 3^{\log_{10}(x/10)}$. Using logarithm properties, $\log_{10}(x/10) = \log_{10} x - \log_{10} 10 = \log_{10} x - 1$. So, the term is $-3^{\log_{10} x - 1} = -\frac{3^{\log_{10} x}}{3}$.

The third term is $9^{\log_{100} x + \log_4 2}$. $\log_{100} x = \log_{10^2} x = \frac{1}{2} \log_{10} x$. $\log_4 2 = \log_{2^2} 2 = \frac{1}{2} \log_2 2 = \frac{1}{2}$. So, the exponent is $\frac{1}{2} \log_{10} x + \frac{1}{2} = \frac{1}{2}(\log_{10} x + 1)$. The term becomes $9^{\frac{1}{2}(\log_{10} x + 1)} = (9^{1/2})^{\log_{10} x + 1} = 3^{\log_{10} x + 1} = 3^{\log_{10} x} \cdot 3^1 = 3 \cdot 3^{\log_{10} x}$.

Substituting these back into the equation: $\log_{10} x - \frac{1}{3} \cdot 3^{\log_{10} x} = 3 \cdot 3^{\log_{10} x}$.

Let $Y = \log_{10} x$. The equation becomes: $Y - \frac{1}{3} \cdot 3^Y = 3 \cdot 3^Y$. $Y = 3 \cdot 3^Y + \frac{1}{3} \cdot 3^Y$. $Y = \left(3 + \frac{1}{3}\right) \cdot 3^Y$. $Y = \frac{10}{3} \cdot 3^Y$.

This is a transcendental equation. Let $f(Y) = Y$ and $g(Y) = \frac{10}{3} \cdot 3^Y$. The derivative of $f(Y)$ is $f'(Y) = 1$. The derivative of $g(Y)$ is $g'(Y) = \frac{10}{3} \cdot 3^Y \cdot \ln 3$. The minimum value of $g(Y) - f(Y)$ occurs when $g'(Y) = f'(Y)$, which is $\frac{10}{3} \cdot 3^Y \cdot \ln 3 = 1$. $3^Y = \frac{3}{10 \ln 3}$. At this minimum, $g(Y) - f(Y) = \frac{10}{3} \cdot \frac{3}{10 \ln 3} - \log_3\left(\frac{3}{10 \ln 3}\right) = \frac{1}{\ln 3} - \frac{\ln(3/(10 \ln 3))}{\ln 3}$. Since $\ln 3 \approx 1.0986$, $10 \ln 3 \approx 10.986$. $3^Y \approx \frac{3}{10.986} \approx 0.273$. $Y = \log_3(0.273) < 0$. The minimum value of $g(Y) - f(Y)$ is approximately $\frac{1}{1.0986} - \frac{\ln(0.273)}{1.0986} \approx 0.91 - \frac{-1.297}{1.0986} \approx 0.91 + 1.18 > 0$. Since the minimum value of $g(Y) - f(Y)$ is positive, $g(Y) > f(Y)$ for all real $Y$. Therefore, the equation $Y = \frac{10}{3} \cdot 3^Y$ has no real solution.

The number '6' at the beginning is likely an equation number. The hint "or x: - $\frac{5}{6}$" is invalid as the argument of a logarithm must be positive. Given the strict interpretation of the question, there is no real solution for $x$.