Question

Let $\left(2+\frac{x^4}{x^2+1}\right)^{10} = A_{20}x^{20} + A_{19}x^{19} + A_{18}x^{18} + .... A_1x + A_0 + \frac{B_1}{x^2+1} + \frac{B_2}{(x^2+1)^2} + ... \frac{B_{10}}{(x^2+1)^{10}}$ where $A_{20}, A_{19}, A_{18},...A_1, A_0, B_1, B_2, ....... B_{10}$ are constants then find $A_0$.

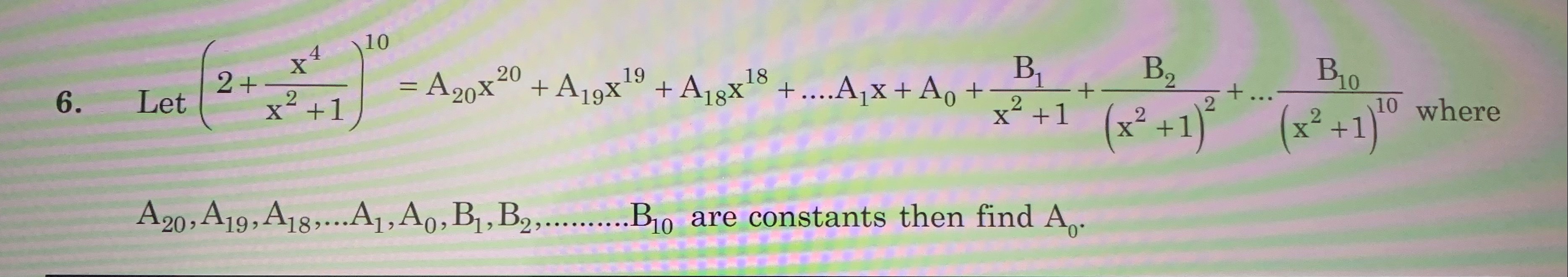
Answer 1

638

Answer 2

We start with

$$\left(2+\frac{x^4}{x^2+1}\right)^{10}=\left(\frac{2(x^2+1)+x^4}{x^2+1}\right)^{10} =\frac{(x^4+2x^2+2)^{10}}{(x^2+1)^{10}}.$$

Notice that

$$x^4+2x^2+2=(x^2+1)^2+1.$$

Thus,

$$(x^4+2x^2+2)^{10} = \left[(x^2+1)^2+1\right]^{10} = \sum_{j=0}^{10} \binom{10}{j}(x^2+1)^{2j}.$$

Dividing by $(x^2+1)^{10}$ gives

$$\left(2+\frac{x^4}{x^2+1}\right)^{10} = \sum_{j=0}^{10} \binom{10}{j}(x^2+1)^{2j-10}.$$

The expression is written as a sum of a polynomial part $Q(x)$ and a fractional part. The polynomial part comes from terms with nonnegative exponents, i.e., $2j-10\ge0$ or $j\ge5$. Hence,

$$Q(x)=\sum_{j=5}^{10} \binom{10}{j}(x^2+1)^{2j-10}.$$

To find $A_0$, the constant term in the polynomial part, set $x=0$:

$$A_0= Q(0)=\sum_{j=5}^{10} \binom{10}{j}(1)^{2j-10}=\sum_{j=5}^{10} \binom{10}{j}.$$

We know that

$$\sum_{j=0}^{10} \binom{10}{j}=2^{10}=1024,$$

and by symmetry,

$$\sum_{j=5}^{10} \binom{10}{j}=\frac{1024+\binom{10}{5}}{2}.$$

Since $\binom{10}{5}=252$,

$$A_0=\frac{1024+252}{2}=\frac{1276}{2}=638.$$