Question
Question: Let $F(x) = \int_{\sin x}^{\cos x} e^{(1+\arcsin t)^2} dt$ on $[0, \frac{\pi}{2}]$ then...
Let F(x)=∫sinxcosxe(1+arcsint)2dt on [0,2π] then
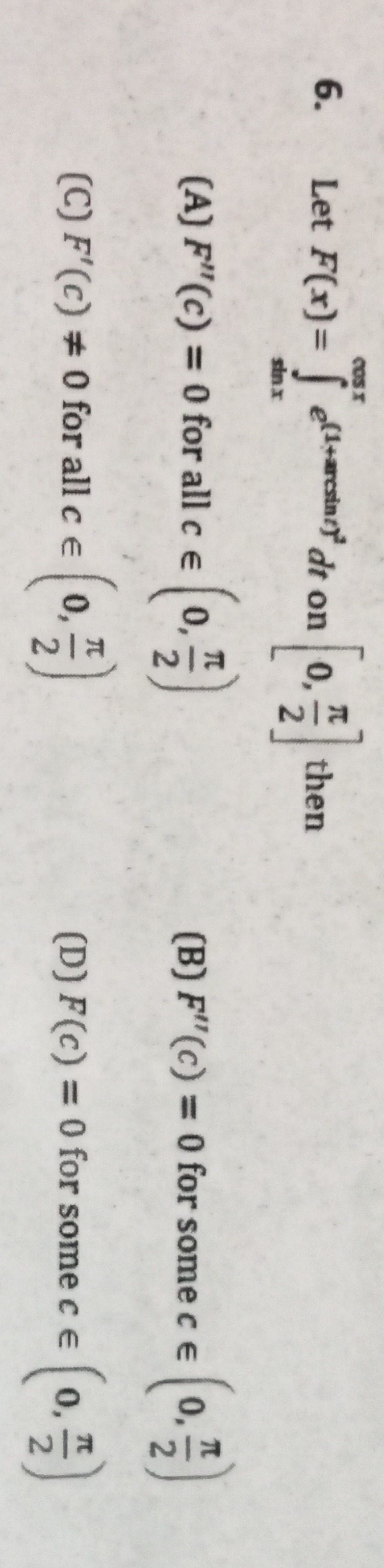
F''(c) = 0 for all c in (0, \frac{\pi}{2})
F''(c) = 0 for some c in (0, \frac{\pi}{2})
F'(c) != 0 for all c in (0, \frac{\pi}{2})
F'(c) = 0 for some c in (0, \frac{\pi}{2})
(B), (C)
Solution
Let f(t)=e(1+arcsint)2. Then F(x)=∫sinxcosxf(t)dt. By the Fundamental Theorem of Calculus and the chain rule, F′(x)=f(cosx)⋅(−sinx)−f(sinx)⋅(cosx). For x∈[0,2π], we have arcsin(cosx)=2π−x and arcsin(sinx)=x. So, F′(x)=−e(1+2π−x)2sinx−e(1+x)2cosx. For x∈(0,2π), sinx>0, cosx>0, and the exponential terms are positive. Thus, −e(1+2π−x)2sinx<0 and −e(1+x)2cosx<0. Therefore, F′(x)<0 for all x∈(0,2π). This implies F′(c)=0 for some c∈(0,2π), making option (C) true and option (D) false.
To analyze F′′(x), we differentiate F′(x): F′′(x)=dxd(−e(1+2π−x)2sinx)−dxd(e(1+x)2cosx) Using the product rule and chain rule: dxd(e(1+2π−x)2sinx)=e(1+2π−x)2⋅2(1+2π−x)(−1)sinx+e(1+2π−x)2cosx =−2(1+2π−x)e(1+2π−x)2sinx+e(1+2π−x)2cosx
dxd(e(1+x)2cosx)=e(1+x)2⋅2(1+x)cosx+e(1+x)2(−sinx) =2(1+x)e(1+x)2cosx−e(1+x)2sinx
F′′(x)=−[−2(1+2π−x)e(1+2π−x)2sinx+e(1+2π−x)2cosx]−[2(1+x)e(1+x)2cosx−e(1+x)2sinx] F′′(x)=2(1+2π−x)e(1+2π−x)2sinx−e(1+2π−x)2cosx−2(1+x)e(1+x)2cosx+e(1+x)2sinx
Consider the limits as x→0+ and x→2π−. As x→0+: F′′(x)≈2(1+2π)e(1+2π)2⋅x−e(1+2π)2⋅1−2(1)e12⋅1+e12⋅0 F′′(x)≈0−e(1+2π)2−2e=−e(1+2π)2−2e. This is negative.
As x→2π− (let x=2π−ϵ for small ϵ>0): 1+2π−x=1+ϵ sinx=sin(2π−ϵ)=cosϵ≈1 cosx=cos(2π−ϵ)=sinϵ≈ϵ 1+x=1+2π−ϵ
F′′(x)≈2(1+ϵ)e(1+ϵ)2⋅1−e(1+ϵ)2⋅ϵ−2(1+2π−ϵ)e(1+2π−ϵ)2⋅ϵ+e(1+2π−ϵ)2⋅1 As ϵ→0+, F′′(x)≈2(1)e12⋅1−e12⋅0−2(1+2π)e(1+2π)2⋅0+e(1+2π)2⋅1 F′′(x)≈2e+e(1+2π)2. This is positive.
Since F′′(x) is continuous on (0,2π) and changes sign from negative to positive, by the Intermediate Value Theorem, there exists some c∈(0,2π) such that F′′(c)=0. Thus, option (B) is true. Option (A) is false because F′′(x) is not identically zero. The correct options are (B) and (C).
