Question
Question: $\int \frac{2x+3}{5x-1} dx$...
∫5x−12x+3dx
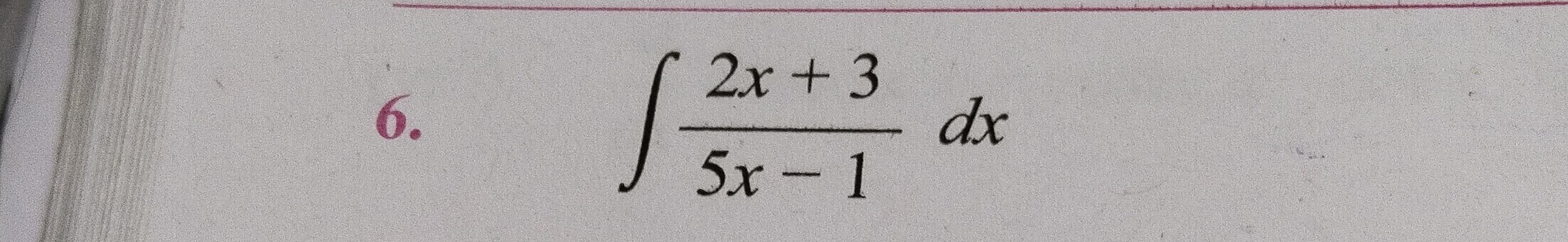
52x+2517ln∣5x−1∣+C
Solution
To integrate the given function, we will use the method of adjusting the numerator to be a multiple of the denominator plus a constant.
Let the given integral be I=∫5x−12x+3dx.
First, we express the numerator (2x+3) in terms of the denominator (5x−1). We want to find constants A and B such that: 2x+3=A(5x−1)+B
Expand the right side: 2x+3=5Ax−A+B
Now, compare the coefficients of x and the constant terms on both sides: Comparing coefficients of x: 5A=2⟹A=52
Comparing constant terms: −A+B=3 Substitute the value of A: −52+B=3 B=3+52 B=515+2=517
Now substitute these values of A and B back into the numerator expression: 2x+3=52(5x−1)+517
Substitute this back into the integral: I=∫5x−152(5x−1)+517dx
Separate the terms in the numerator: I=∫(5x−152(5x−1)+5x−1517)dx I=∫(52+5(5x−1)17)dx
Now, integrate term by term: I=∫52dx+∫5(5x−1)17dx I=52∫1dx+517∫5x−11dx
The first integral is straightforward: ∫1dx=x
For the second integral, ∫5x−11dx, we use a substitution. Let u=5x−1. Then, differentiate u with respect to x: dxdu=5 du=5dx⟹dx=51du
Substitute u and dx into the integral: ∫u1(51du)=51∫u1du We know that ∫u1du=ln∣u∣+C′ So, 51ln∣u∣+C′=51ln∣5x−1∣+C′
Now, combine all parts of the integral: I=52x+517(51ln∣5x−1∣)+C I=52x+2517ln∣5x−1∣+C where C is the constant of integration.
