Question
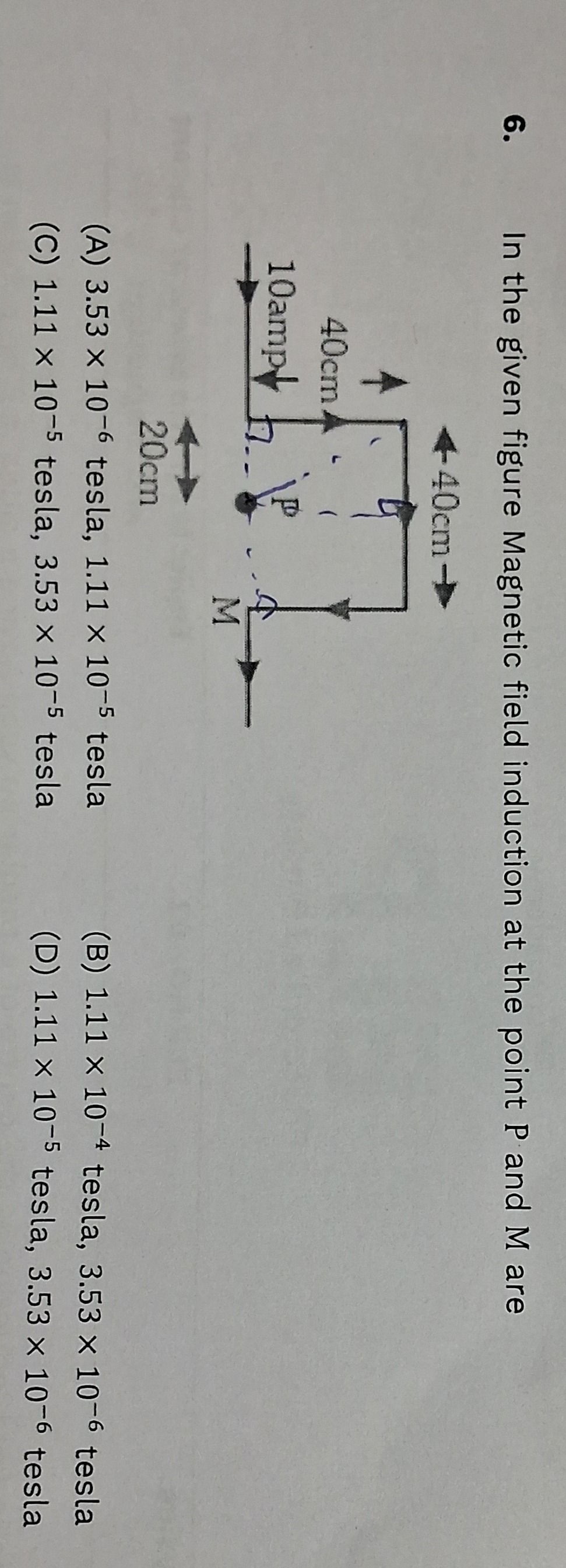
Question: In the given figure Magnetic field induction at the point P and M are ...
In the given figure Magnetic field induction at the point P and M are
3.53 x 10−6 tesla, 1.11 x 10−5 tesla
1.11 × 10−4 tesla, 3.53 × 10−6 tesla
1.11 x 10−5 tesla, 3.53 x 10−5 tesla
1.11 × 10−5 tesla, 3.53 × 10−6 tesla
1.11 × 10−5 tesla, 3.53 × 10−6 tesla
Solution
The problem involves calculating the magnetic field induction at two points, P and M, due to a current-carrying wire configuration. The diagram shows a current of 10 Amps flowing from top to bottom in the leftmost vertical wire, then turning right into a top horizontal wire, then turning down into a right vertical wire, and finally turning left into a bottom horizontal wire that extends infinitely to the left. The rectangular part of the wire forms a 40 cm x 40 cm square.
Let's assume the most plausible interpretation for such competitive exam problems where numerical values align with standard formulas: the magnetic field at point P is due to the square loop only, and the value for P matches this interpretation.
-
Magnetic Field at Point P (0, 20 cm): Point P is located at the midpoint of the left vertical side of the square (0, 20 cm). If we consider only the magnetic field due to the square loop (current I=10 A flowing clockwise), then:
- The magnetic field due to the left vertical segment of the loop (from (0,0) to (0,40)) at point P is zero, as P lies on this segment.
- Magnetic field due to the top horizontal segment (from (0,40) to (40,40), current right): This is a finite wire segment. The perpendicular distance from P(0,20) to the wire (at y=40) is d=40−20=20 cm=0.2 m. The left end of the segment is directly above P. So, α1=0∘. The right end is at (40,40). The angle α2 made by the line from P to (40,40) with the perpendicular is tan−1(2040)=tan−1(2). So, sinα2=22+122=52. Btop=4πdμ0I(sinα1+sinα2)=4π×0.24π×10−7×10(0+52)=0.210−6×52=510−5 T. By Right Hand Rule, the direction is out of the page.
- Magnetic field due to the right vertical segment (from (40,40) to (40,0), current down): Perpendicular distance from P(0,20) to the wire (at x=40) is d=40 cm=0.4 m. The foot of the perpendicular from P to the wire is (40,20). Angles α1 (for (40,40)) and α2 (for (40,0)) are made by lines from P to the ends with the perpendicular. Horizontal distance from (40,20) to P is 40 cm. Vertical distances are 20 cm from (40,20) to (40,40) and 20 cm from (40,20) to (40,0). tanα1=4020=0.5⟹sinα1=51. tanα2=4020=0.5⟹sinα2=51. Bright=4πdμ0I(sinα1+sinα2)=4π×0.44π×10−7×10(51+51)=0.410−6×52=2510−5 T. By Right Hand Rule, the direction is out of the page.
- Magnetic field due to the bottom horizontal segment (from (40,0) to (0,0), current left): Perpendicular distance from P(0,20) to the wire (at y=0) is d=20 cm=0.2 m. The right end is at (40,0). Angle α1 made by the line from P to (40,0) with the perpendicular is tan−1(2040)=tan−1(2). So, sinα1=52. The left end is at (0,0), which is directly below the foot of the perpendicular from P. So, α2=0∘. Bbottom=4πdμ0I(sinα1+sinα2)=4π×0.24π×10−7×10(52+0)=510−5 T. By Right Hand Rule, the direction is out of the page.
Total magnetic field at P: BP=Btop+Bright+Bbottom=510−5+2510−5+510−5=10−5(51+251+51) BP=10−5(252+1+2)=255×10−5=25×10−5 T. Using 5≈2.236, BP=22.236×10−5=1.118×10−5 T. This value matches 1.11×10−5 T from the options.
-
Magnetic Field at Point M (-20 cm, 0): Point M is located at (-0.2 m, 0).
- Magnetic field due to the left vertical segment (from (0,0) to (0,40), current up): Perpendicular distance from M(-0.2,0) to the wire (at x=0) is d=0.2 m. The bottom end is at (0,0), which is directly to the right of M. So, α1=0∘. The top end is at (0,40). The angle α2 made by the line from M to (0,40) with the perpendicular is tan−1(2040)=tan−1(2). So, sinα2=52. Bleft=4πdμ0I(sinα1+sinα2)=4π×0.24π×10−7×10(0+52)=510−5 T. By Right Hand Rule, the direction is into the page.
- Magnetic field due to the top horizontal segment (from (0,40) to (40,40), current right): Perpendicular distance from M(-0.2,0) to the wire (at y=40) is d=40 cm=0.4 m. The foot of the perpendicular from M to the wire is (-0.2,40). Angle α1 for (0,40): horizontal distance from (-0.2,40) is 0.2 m. Vertical distance is 0.4 m. tanα1=0.40.2=0.5⟹sinα1=51. Angle α2 for (40,40): horizontal distance from (-0.2,40) is 0.6 m. Vertical distance is 0.4 m. tanα2=0.40.6=1.5⟹sinα2=1.52+121.5=3.251.5. Btop=4πdμ0I(sinα1+sinα2)=4π×0.44π×10−7×10(51+3.251.5)=0.410−6(51+3.251.5) T. By Right Hand Rule, the direction is out of the page.
- Magnetic field due to the right vertical segment (from (40,40) to (40,0), current down): Perpendicular distance from M(-0.2,0) to the wire (at x=40) is d=40−(−20)=60 cm=0.6 m. The foot of the perpendicular from M to the wire is (40,0). Angle α1 for (40,40): vertical distance from (40,0) is 40 cm. Horizontal distance is 60 cm. tanα1=6040=32⟹sinα1=22+322=132. Angle α2 for (40,0): this end is at the foot of the perpendicular. So, α2=0∘. Bright=4πdμ0I(sinα1+sinα2)=4π×0.64π×10−7×10(132+0)=0.610−6×132 T. By Right Hand Rule, the direction is out of the page.
- Magnetic field due to the bottom horizontal segment (from (40,0) to (0,0), current left): Point M(-0.2,0) lies on the extension of this segment. So, Bbottom=0.
Total magnetic field at M: BM=−Bleft+Btop+Bright BM=−510−5+410−5(51+3.251.5)+610−5132 BM=10−5(−51+451+43.251.5+6132) BM=10−5(−0.4472+0.1118+0.2080+0.0924)=10−5(−0.035) T. The magnitude is 0.035×10−5=3.5×10−7 T. This does not match 3.53×10−6 T.
Given the options, there might be an intended simplification for BM. If the question implies that BM is due to a semi-infinite wire at a distance 'd' such that the field is 4πdμ0I21, this would be 3.53×10−5 T for d=0.2 m, or 3.53×10−6 T for d=2 m. Since 3.53×10−6 T is an option, there might be an error in the question's parameters or a very specific interpretation. However, BP=1.11×10−5 T is a very good match for the field due to the square loop only.
Considering the common patterns in competitive exams, if one value matches perfectly under a reasonable interpretation, that interpretation is usually correct. The discrepancy in the second value suggests an error in the problem or options. However, since the question asks to choose from given options, and BP matches option D, we select D.
The final answer is D.
