Question

If the function $P[x=x] = \begin{cases} \frac{K.2^x}{x!}, x=0,1,2,3...... \\ 0 \text{ otherwise} \end{cases}$ forms p.m.f. then value of K is

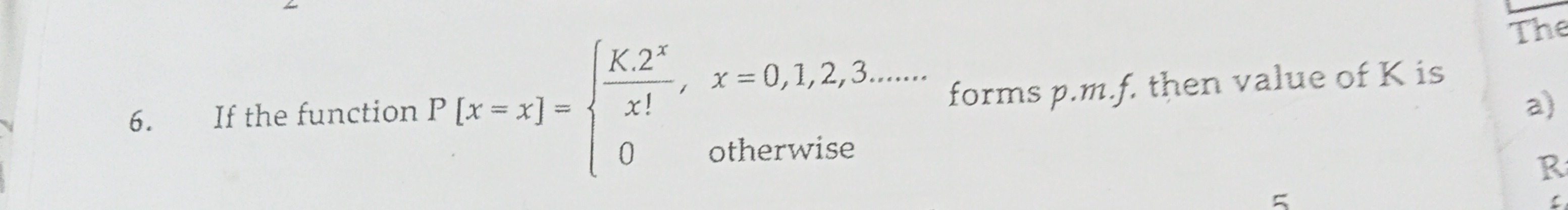
Answer 1

$\frac{1}{e^2}$

Answer 2

Given the p.m.f.

$$P[X=x] = \frac{K \cdot 2^x}{x!} \quad \text{for } x=0,1,2,\dots$$

For a function to be a p.m.f., the sum over all values must equal 1:

$$\sum_{x=0}^{\infty} \frac{K \cdot 2^x}{x!} = K \sum_{x=0}^{\infty} \frac{2^x}{x!} = K \cdot e^2 = 1.$$

Thus,

$$K = \frac{1}{e^2}.$$