Solveeit Logo
Login

Question

Question: If PSQ is a focal chord of parabola whose focus at S and A is a point on the parabola such that the ...

If PSQ is a focal chord of parabola whose focus at S and A is a point on the parabola such that the lines through PA and QA meets the directrix of the parabola at B(3,-1), C(0,2) respectively and the axis of the parabola is x-y=0 then the possible coordinates of the focus of the parabola is/are

A

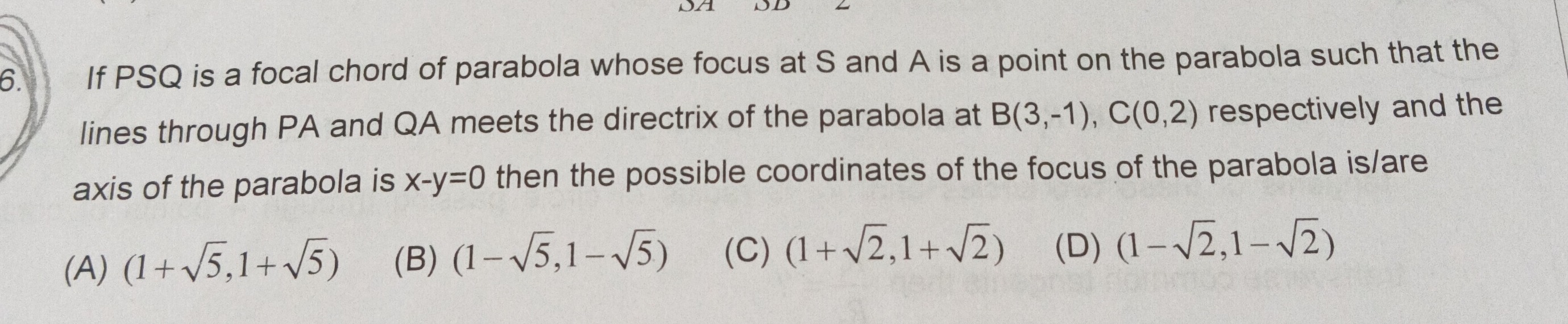
(1+5,1+5)(1+\sqrt{5},1+\sqrt{5})

B

(1−5,1−5)(1-\sqrt{5},1-\sqrt{5})

C

(1+2,1+2)(1+\sqrt{2},1+\sqrt{2})

D

(1−2,1−2)(1-\sqrt{2},1-\sqrt{2})

Answer

(C), (D)

Explanation

Solution

The problem involves properties of a parabola, specifically related to its focal chord, focus, directrix, and axis.

Key Property: A crucial property of a parabola is that if PSQ is a focal chord (P, Q are points on the parabola, and S is the focus), and A is any point on the parabola, then the lines PA and QA intersect the directrix at points B and C respectively, such that the angle ∠BSC=90∘\angle BSC = 90^\circ.

Applying the Property:

  1. Directrix Equation: We are given the coordinates of B(3, -1) and C(0, 2), and these points lie on the directrix. Therefore, the line passing through B and C is the directrix. The slope of BC is mBC=2−(−1)0−3=3−3=−1m_{BC} = \frac{2 - (-1)}{0 - 3} = \frac{3}{-3} = -1. The equation of the directrix (line BC) using point-slope form with C(0, 2) is: y−2=−1(x−0)y - 2 = -1(x - 0) y−2=−xy - 2 = -x x+y−2=0x + y - 2 = 0.

  2. Focus Coordinates and Right Angle Condition: Let the focus be S(xS,yS)S(x_S, y_S). According to the property, ∠BSC=90∘\angle BSC = 90^\circ. This means the vectors SB⃗\vec{SB} and SC⃗\vec{SC} are perpendicular, so their dot product is zero. SB⃗=B−S=(3−xS,−1−yS)\vec{SB} = B - S = (3 - x_S, -1 - y_S) SC⃗=C−S=(0−xS,2−yS)=(−xS,2−yS)\vec{SC} = C - S = (0 - x_S, 2 - y_S) = (-x_S, 2 - y_S) SB⃗⋅SC⃗=(3−xS)(−xS)+(−1−yS)(2−yS)=0\vec{SB} \cdot \vec{SC} = (3 - x_S)(-x_S) + (-1 - y_S)(2 - y_S) = 0 −3xS+xS2+(−2+yS−2yS+yS2)=0-3x_S + x_S^2 + (-2 + y_S - 2y_S + y_S^2) = 0 xS2+yS2−3xS−yS−2=0x_S^2 + y_S^2 - 3x_S - y_S - 2 = 0 (Equation 1)

  3. Axis of the Parabola: The axis of the parabola is given by the equation x−y=0x - y = 0. The focus S must lie on the axis of the parabola. Therefore, xS−yS=0  ⟹  xS=ySx_S - y_S = 0 \implies x_S = y_S (Equation 2).

  4. Solving for Focus Coordinates: Substitute yS=xSy_S = x_S from Equation 2 into Equation 1: xS2+xS2−3xS−xS−2=0x_S^2 + x_S^2 - 3x_S - x_S - 2 = 0 2xS2−4xS−2=02x_S^2 - 4x_S - 2 = 0 Divide by 2: xS2−2xS−1=0x_S^2 - 2x_S - 1 = 0 Use the quadratic formula to solve for xSx_S: xS=−(−2)±(−2)2−4(1)(−1)2(1)x_S = \frac{-(-2) \pm \sqrt{(-2)^2 - 4(1)(-1)}}{2(1)} xS=2±4+42x_S = \frac{2 \pm \sqrt{4 + 4}}{2} xS=2±222x_S = \frac{2 \pm 2\sqrt{2}}{2} xS=1±2x_S = 1 \pm \sqrt{2}

    Since yS=xSy_S = x_S, the possible coordinates for the focus S are:

    • If xS=1+2x_S = 1 + \sqrt{2}, then yS=1+2y_S = 1 + \sqrt{2}. So, S1=(1+2,1+2)S_1 = (1 + \sqrt{2}, 1 + \sqrt{2}).
    • If xS=1−2x_S = 1 - \sqrt{2}, then yS=1−2y_S = 1 - \sqrt{2}. So, S2=(1−2,1−2)S_2 = (1 - \sqrt{2}, 1 - \sqrt{2}).

Comparing these results with the given options: (A) (1+5,1+5)(1+\sqrt{5},1+\sqrt{5}) (B) (1−5,1−5)(1-\sqrt{5},1-\sqrt{5}) (C) (1+2,1+2)(1+\sqrt{2},1+\sqrt{2}) (D) (1−2,1−2)(1-\sqrt{2},1-\sqrt{2})

Both options (C) and (D) are possible coordinates for the focus.