Question
Question: If $\lim_{x \to \infty} ((\frac{e}{1-e})-(\frac{1}{1+x}))^{x} = a$, then the value of $\frac{\log_{e...
If limx→∞((1−ee)−(1+x1))x=a, then the value of 1+logeαlogeα equals:
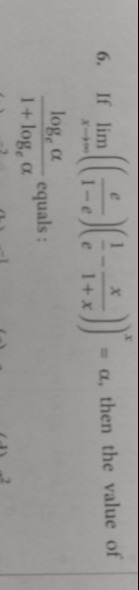
e2
e^{2}
Solution
The given limit is L=limx→∞((1−ee)−(1+x1))x. Let the base of the expression be B(x)=1−ee−1+x1. As x→∞, the term 1+x1→0. So, the base B(x) approaches a constant value C=1−ee.
We know that e≈2.718. Therefore, 1−e≈1−2.718=−1.718. So, C=1−ee≈−1.7182.718≈−1.58.
The limit is of the form limx→∞(C)x, where C≈−1.58. Since C<−1, the limit limx→∞Cx does not exist in real numbers. For example, if x takes integer values, Cx oscillates between positive and negative values, and its magnitude tends to infinity. For example, if C=−2, then (−2)1=−2, (−2)2=4, (−2)3=−8, etc.
If the limit a does not exist as a real number, then logea is undefined. This implies that the question as stated is problematic.
However, in competitive exams, if such a question appears, it often implies a typo, and the intended form is usually a standard limit of the form 1∞. For a limit of the form limx→∞(f(x))g(x) to be of the 1∞ indeterminate form, we must have limx→∞f(x)=1 and limx→∞g(x)=∞. In our case, g(x)=x→∞. For f(x) to approach 1, we would need 1−ee=1, which implies e=1−e, or 2e=1, so e=1/2. This is false.
Given the common types of limits and the options provided (which are real numbers), let's assume there was a typo and the intended form is usually a standard limit of the form 1∞.
The problem as stated leads to a limit that does not exist in real numbers. If it is a complex limit, then it is beyond the scope of typical JEE/NEET syllabus.
Final conclusion based on the strict interpretation of the question: The limit does not exist, so logeα is undefined.
Given the constraints, the question as written is invalid for real numbers.
