Question
Question: If $I_{m,n} = \int cos^m x cos nx dx$, then show that: $I_{m,n} = \frac{cos^m x sin nx}{m+n} + \frac...
If Im,n=∫cosmxcosnxdx, then show that: Im,n=m+ncosmxsinnx+m+nmIm−1,n−1
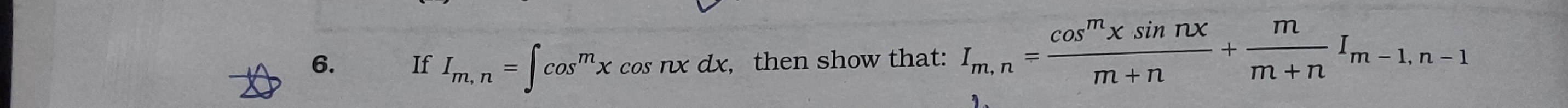
m+ncosmxsinnx+m+nmIm−1,n−1
Solution
To derive the reduction formula for Im,n=∫cosmxcosnxdx, we use integration by parts.
Let u=cosmx and dv=cosnxdx. Then, we find du and v: du=mcosm−1x(−sinx)dx=−mcosm−1xsinxdx v=∫cosnxdx=nsinnx
Applying the integration by parts formula ∫udv=uv−∫vdu: Im,n=cosmx(nsinnx)−∫(nsinnx)(−mcosm−1xsinx)dx Im,n=ncosmxsinnx+nm∫cosm−1xsinxsinnxdx
Now, we need to simplify the integral term ∫cosm−1xsinxsinnxdx. We use the trigonometric identity: cos(A−B)=cosAcosB+sinAsinB. Let A=nx and B=x. Then cos(nx−x)=cosnxcosx+sinnxsinx. Rearranging this to find sinnxsinx: sinnxsinx=cos(n−1)x−cosnxcosx
Substitute this identity into the integral: ∫cosm−1xsinxsinnxdx=∫cosm−1x(cos(n−1)x−cosnxcosx)dx =∫cosm−1xcos(n−1)xdx−∫cosm−1xcosnxcosxdx The first integral is Im−1,n−1. The second integral is ∫cosmxcosnxdx, which is Im,n. So, ∫cosm−1xsinxsinnxdx=Im−1,n−1−Im,n.
Substitute this back into the expression for Im,n: Im,n=ncosmxsinnx+nm(Im−1,n−1−Im,n) Im,n=ncosmxsinnx+nmIm−1,n−1−nmIm,n
Now, collect the Im,n terms on the left side: Im,n+nmIm,n=ncosmxsinnx+nmIm−1,n−1 Im,n(1+nm)=ncosmxsinnx+nmIm−1,n−1 Im,n(nn+m)=ncosmxsinnx+nmIm−1,n−1
Finally, multiply both sides by m+nn to isolate Im,n: Im,n=m+nn(ncosmxsinnx+nmIm−1,n−1) Im,n=m+ncosmxsinnx+m+nmIm−1,n−1
This completes the proof of the reduction formula.
