Question

If 0.5 M methanol undergo self dissociation like $CH_3OH \rightleftharpoons CH_3O^- + H^+$ & if concentration of H$^+$ is 2.5 × $10^{-4}$ M then calculate % dissociation of methanol.

Answer 1

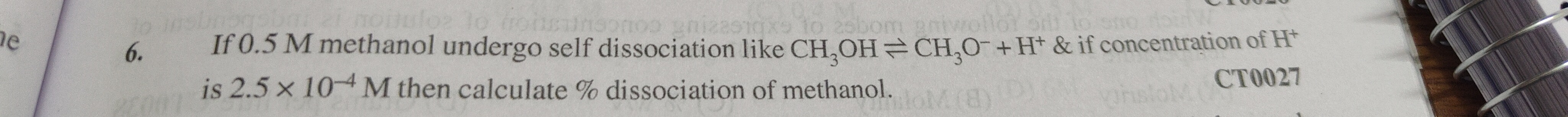
0.05%

Answer 2

The self-dissociation of methanol can be represented by the following equilibrium:

$CH_3OH \rightleftharpoons CH_3O^- + H^+$

Let's set up an ICE (Initial, Change, Equilibrium) table for the dissociation:

Initial concentration of $CH_3OH = 0.5$ M

Species	Initial (M)	Change (M)	Equilibrium (M)
$CH_3OH$	0.5	$-x$	$0.5 - x$
$CH_3O^-$	0	$+x$	$x$
$H^+$	0	$+x$	$x$

We are given that the concentration of $H^+$ at equilibrium is $2.5 \times 10^{-4}$ M. From the ICE table, at equilibrium, $[H^+] = x$. Therefore, $x = 2.5 \times 10^{-4}$ M.

The percentage dissociation ($\alpha$) is calculated as the ratio of the concentration of methanol that dissociated to its initial concentration, multiplied by 100.

$\% \text{ dissociation} = \frac{\text{concentration dissociated}}{\text{initial concentration}} \times 100\%$

In this case, the concentration dissociated is $x$.

$\% \text{ dissociation} = \frac{x}{0.5} \times 100\%$

Substitute the value of $x$:

$\% \text{ dissociation} = \frac{2.5 \times 10^{-4}}{0.5} \times 100\%$

$\% \text{ dissociation} = \frac{2.5}{0.5} \times 10^{-4} \times 100\%$

$\% \text{ dissociation} = 5 \times 10^{-4} \times 10^2 \%$

$\% \text{ dissociation} = 5 \times 10^{-2} \%$

$\% \text{ dissociation} = 0.05 \%$

The percentage dissociation of methanol is 0.05%.