Question
Question: Graph shows three waves that are separately sent along a string that is stretched under a certain te...
Graph shows three waves that are separately sent along a string that is stretched under a certain tension along x-axis. If ω1,ω2 and ω3 are their angular frequencies respectively then :-
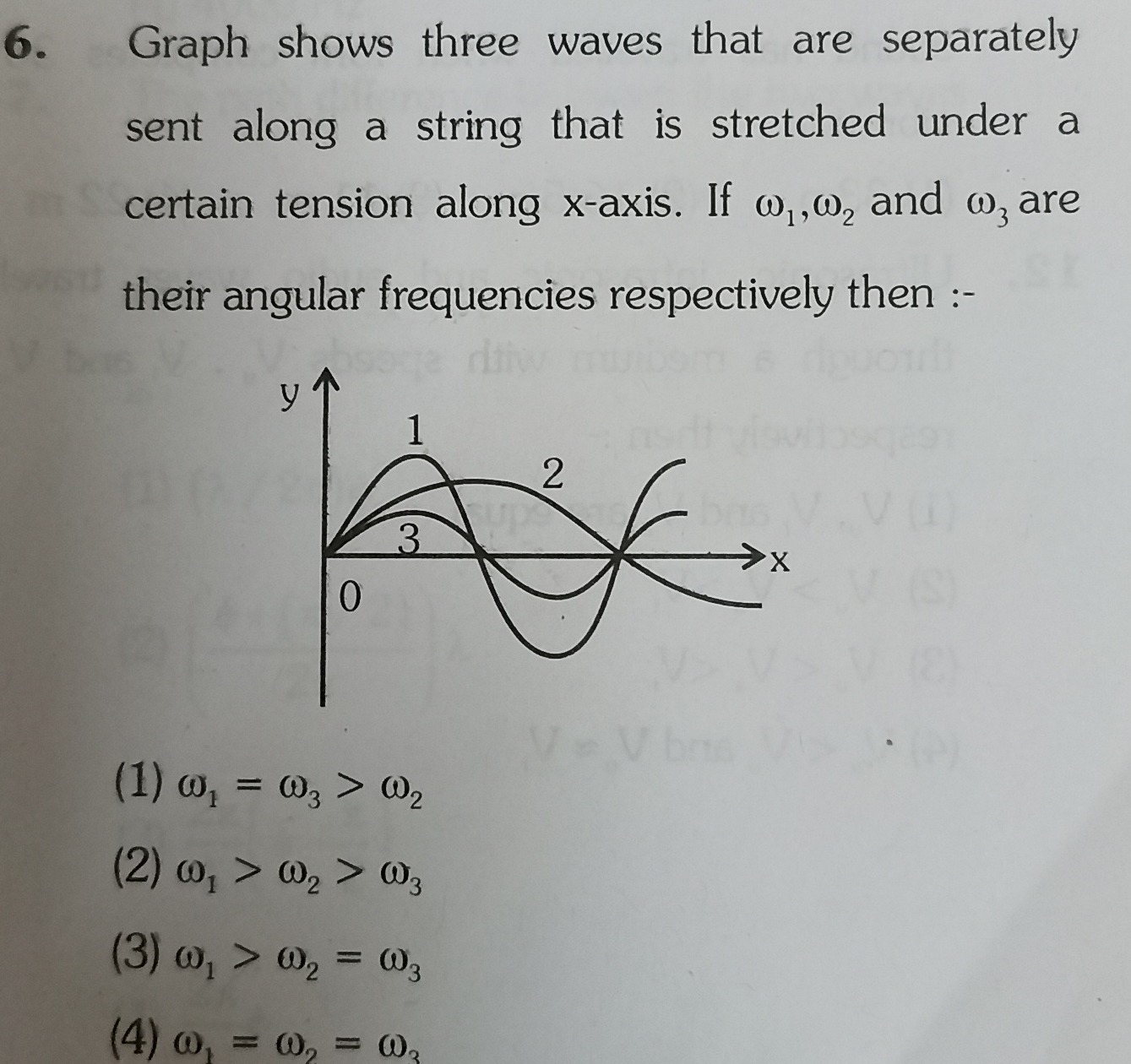
ω1=ω3>ω2
ω1>ω2>ω3
ω1>ω2=ω3
ω1=ω2=ω3
ω1>ω2>ω3
Solution
The speed of transverse waves on a string is given by v=T/μ, where T is the tension and μ is the linear mass density. Since all three waves are sent along the same string under the same tension, their speeds (v) are equal. The angular frequency (ω), wave speed (v), and wavelength (λ) are related by the equation ω=vκ, where κ is the wave number, and κ=2π/λ. Thus, ω=2πv/λ.
From the graph, we can observe the wavelengths of the three waves. The wavelength is the spatial period of the wave. By visually inspecting the graph, we can see that for a given horizontal distance, wave 1 completes more oscillations than wave 2, and wave 2 completes more oscillations than wave 3. This means that wave 1 has the shortest wavelength (λ1), wave 2 has a medium wavelength (λ2), and wave 3 has the longest wavelength (λ3). Therefore, λ1<λ2<λ3.
Since the wave speed v is constant for all three waves, and ω=2πv/λ, the angular frequency ω is inversely proportional to the wavelength λ. As λ1<λ2<λ3, it follows that 1/λ1>1/λ2>1/λ3. Multiplying by the constant 2πv, we get: λ12πv>λ22πv>λ32πv This implies ω1>ω2>ω3.
