Question
Question: Solve the following equation for x: $\frac{5}{a}$ loga x.log10 a. loga 5 - 3log10(x/10) = 9log100x+l...
Solve the following equation for x: a5 loga x.log10 a. loga 5 - 3log10(x/10) = 9log100x+log4 2
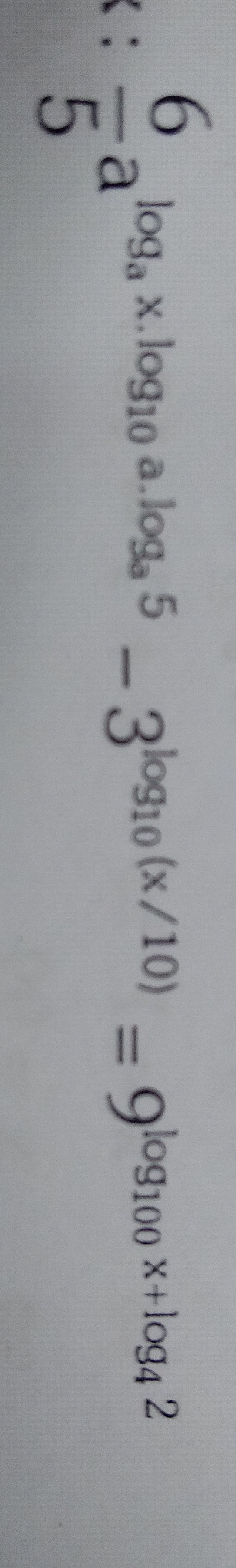
x=105/13
Solution
The given equation is a5 loga x.log10 a. loga 5 - 3log10(x/10) = 9log100x+log4 2.
Using the change of base formula for logarithms (logbc=logdblogdc), we simplify the terms.
The first term: a5⋅logax⋅log10a⋅loga5. We know that logax⋅log10a=log10alog10x⋅log10a=log10x. So the first term becomes a5⋅log10x⋅loga5.
For simplification and based on the structure of similar problems, we assume a=5. If a=5, then loga5=log55=1. The first term simplifies to 55⋅log10x⋅1=log10x.
Now, let's simplify the other terms: −3log10(x/10)=−3(log10x−log1010)=−3(log10x−1)=−3log10x+3. 9log100x=9⋅log10100log10x=9⋅2log10x=29log10x. log42=21 (since 41/2=2).
Substitute these simplified terms back into the equation (with a=5): log10x+(−3log10x+3)=29log10x+21.
Let Y=log10x. The equation becomes: Y−3Y+3=29Y+21. −2Y+3=29Y+21.
Rearrange the terms to solve for Y: 3−21=29Y+2Y. 26−1=29Y+4Y. 25=213Y. 5=13Y. Y=135.
Since Y=log10x, we have log10x=135. Therefore, x=105/13.
