Question

Find locus of points of intersection of perpendicular tangents to parabolas.

(i) $(y-4)^2 = 4(x-3)$ (ii) $x^2-4x-8y+12=0$

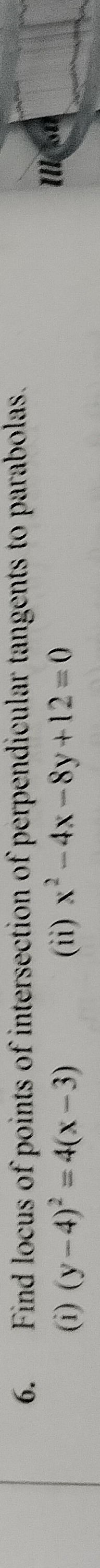
Answer 1

(2, -1)

Answer 2

The locus of the intersection of perpendicular tangents to a parabola is its directrix.

For the first parabola, $(y-4)^2 = 4(x-3)$, which is in the standard form $(y-k)^2 = 4a(x-h)$. The vertex is $(h, k) = (3, 4)$ and $4a = 4 \implies a=1$. The directrix is $x = h - a = 3 - 1 = 2$.

For the second parabola, $x^2-4x-8y+12=0$. Completing the square, we get $(x-2)^2 = 8(y-1)$. This is in the standard form $(x-h)^2 = 4a(y-k)$. The vertex is $(h, k) = (2, 1)$ and $4a = 8 \implies a=2$. The directrix is $y = k - a = 1 - 2 = -1$.

The question asks for the locus of points satisfying the condition for both parabolas, which is the intersection of their directrices. The intersection of $x=2$ and $y=-1$ is the point $(2, -1)$.