Question
Question: Evaluate the integral $$ \int_{0}^{\infty} \int_{0}^{\infty} \frac{dx\,dy}{(1+x^2+y^2)^2} $$...
Evaluate the integral ∫0∞∫0∞(1+x2+y2)2dxdy
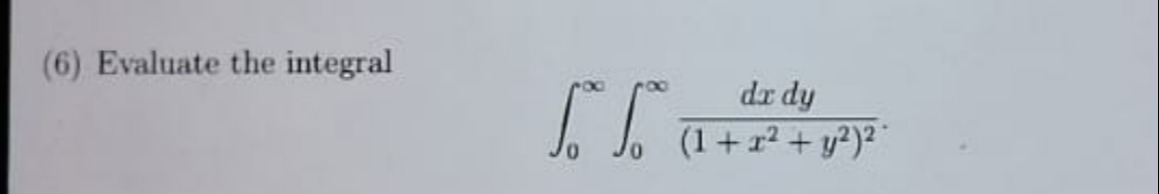
Answer
4π
Explanation
Solution
The integral is transformed into polar coordinates, where x=rcosθ, y=rsinθ, and dxdy=rdrdθ. The first quadrant (x≥0,y≥0) corresponds to r∈[0,∞) and θ∈[0,π/2]. The integral becomes ∫0π/2∫0∞(1+r2)2rdrdθ. This is separated into an angular integral (∫0π/2dθ=π/2) and a radial integral (∫0∞(1+r2)2rdr). Using the substitution u=1+r2 for the radial integral, we get 21∫1∞u−2du=21. The final result is the product of these two values: (π/2)×(1/2)=π/4.
