Question

Consider the polynomial $P(x) = \prod_{k=0}^{10} (x^{2^k} + 2^k) = (x+1)(x^2+2)(x^4+4)....(x^{1024}+1024)$.

The coefficient of $x^{2016}$ is $4^n$, then value of n is

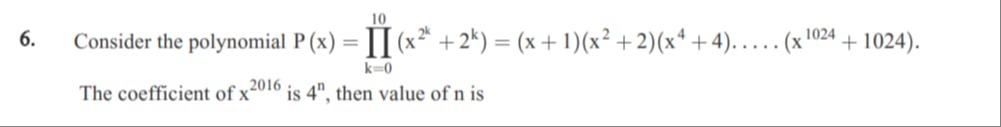
Answer 1

5

Answer 2

We have:

$$P(x)=\prod_{k=0}^{10} (x^{2^k}+2^k)$$

The maximum power of $x$ is:

$$\sum_{k=0}^{10} 2^k = 2047.$$

To get $x^{2016}$, we must miss an exponent sum of:

$$2047-2016 = 31.$$

Express 31 in binary:

$$31 = 1+2+4+8+16 = 2^0+2^1+2^2+2^3+2^4.$$

Thus, for $k=0,1,2,3,4$ we choose the constant term $2^k$ and for $k=5,6,\ldots,10$ we choose $x^{2^k}$.

The coefficient becomes:

$$2^0 \cdot 2^1 \cdot 2^2 \cdot 2^3 \cdot 2^4 = 2^{(0+1+2+3+4)} = 2^{10}=1024.$$

Given that the coefficient equals $4^n$ and since $4^n = 2^{2n}$, we have:

$$2^{2n} = 2^{10} \quad \Rightarrow \quad 2n=10 \quad \Rightarrow \quad n=5.$$