Solveeit Logo
Login

Question

Question: $\begin{vmatrix} 1 & 1 & 1 \\ a & b & c \\ a^2 & b^2 & c^2 \end{vmatrix} =$...

∣111abca2b2c2∣=\begin{vmatrix} 1 & 1 & 1 \\ a & b & c \\ a^2 & b^2 & c^2 \end{vmatrix} =

A

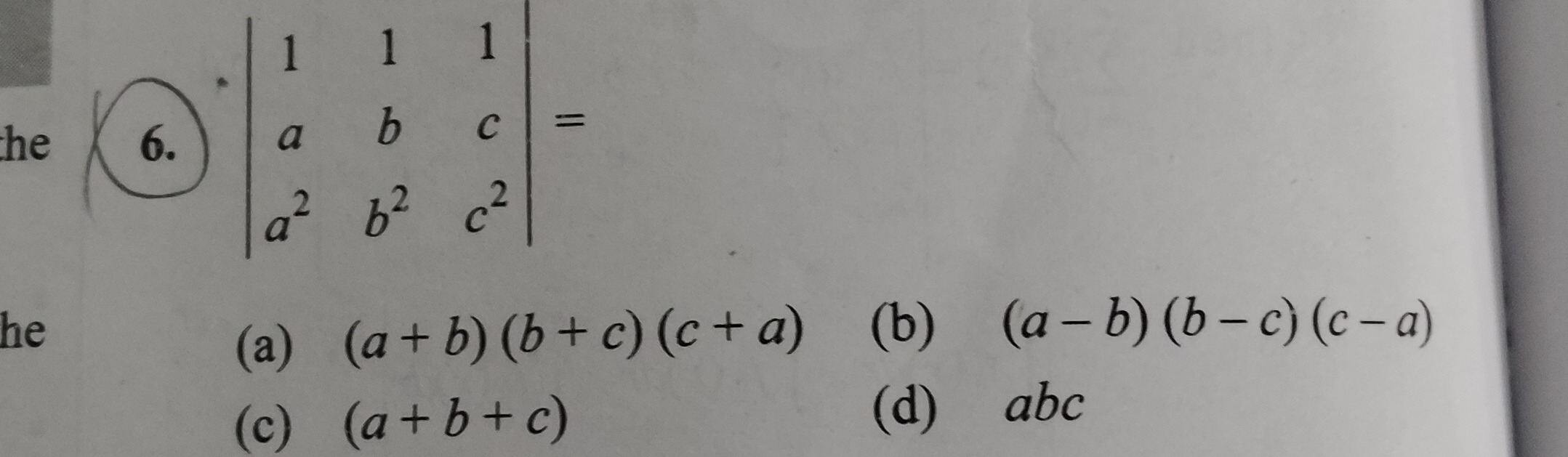
(a+b)(b+c)(c+a)(a + b) (b + c) (c + a)

B

(a−b)(b−c)(c−a)(a - b) (b - c) (c - a)

C

(a+b+c)(a+b+c)

D

abcabc

Answer

(a - b) (b - c) (c - a)

Explanation

Solution

The given determinant is a Vandermonde determinant. We can evaluate it by performing column operations.

Step 1: Perform column operations to introduce zeros.

Apply the operations C2→C2−C1C_2 \rightarrow C_2 - C_1 and C3→C3−C1C_3 \rightarrow C_3 - C_1:

D=∣11−11−1ab−ac−aa2b2−a2c2−a2∣=∣100ab−ac−aa2(b−a)(b+a)(c−a)(c+a)∣D = \begin{vmatrix} 1 & 1-1 & 1-1 \\ a & b-a & c-a \\ a^2 & b^2-a^2 & c^2-a^2 \end{vmatrix} = \begin{vmatrix} 1 & 0 & 0 \\ a & b-a & c-a \\ a^2 & (b-a)(b+a) & (c-a)(c+a) \end{vmatrix}

Step 2: Expand the determinant along the first row (R1R_1).

Since the first row has two zeros, the expansion simplifies significantly:

D=1⋅∣b−ac−a(b−a)(b+a)(c−a)(c+a)∣D = 1 \cdot \begin{vmatrix} b-a & c-a \\ (b-a)(b+a) & (c-a)(c+a) \end{vmatrix}

Step 3: Factor out common terms from the columns of the 2x2 determinant.

Notice that (b−a)(b-a) is a common factor in the first column and (c−a)(c-a) is a common factor in the second column of the 2x2 determinant.

D=(b−a)(c−a)∣11b+ac+a∣D = (b-a)(c-a) \begin{vmatrix} 1 & 1 \\ b+a & c+a \end{vmatrix}

Step 4: Evaluate the remaining 2x2 determinant.

The determinant of a 2x2 matrix ∣pqrs∣\begin{vmatrix} p & q \\ r & s \end{vmatrix} is ps−qrps - qr.

D=(b−a)(c−a)[1⋅(c+a)−1⋅(b+a)]=(b−a)(c−a)[c+a−b−a]=(b−a)(c−a)[c−b]D = (b-a)(c-a) [1 \cdot (c+a) - 1 \cdot (b+a)] = (b-a)(c-a) [c+a - b-a] = (b-a)(c-a) [c-b]

Step 5: Rearrange the terms to match the given options.

The calculated result is (b−a)(c−a)(c−b)(b-a)(c-a)(c-b). We can rewrite the terms in our result:

(b−a)=−(a−b)(b-a) = -(a-b) (c−b)=−(b−c)(c-b) = -(b-c)

Substitute these into the expression for D:

D=(−(a−b))(c−a)(−(b−c))=(−1)⋅(−1)⋅(a−b)(c−a)(b−c)=(a−b)(b−c)(c−a)D = (-(a-b)) (c-a) (-(b-c)) = (-1) \cdot (-1) \cdot (a-b)(c-a)(b-c) = (a-b)(b-c)(c-a)

This matches option (b).