Question
Question: An ideal smooth massless inextensible string passes through a bead of mass m as shown whose ends are...
An ideal smooth massless inextensible string passes through a bead of mass m as shown whose ends are fixed at A and B. Initially the system is in equilibrium. Now the bead is given a velocity 2gl in horizontal direction and in the plane of the string as shown. Let T0 be the tension in the string and r0 be the radius of curvature of path of bead just after the velocity is given. Then choose the correct option(s).
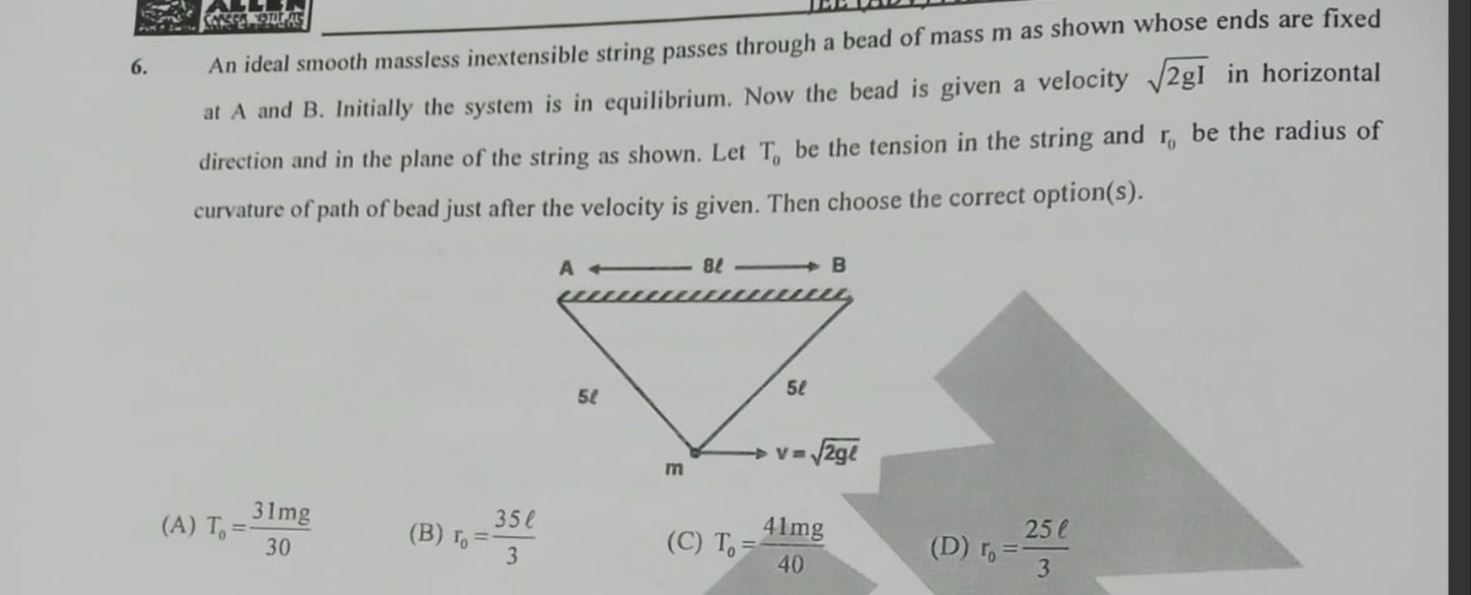
T0=3031mg
r0=335l
T0=4041mg
r0=325l
Options (A) and (B) are correct.
Solution
The solution involves a careful "impulsive-constraint" analysis using energy-momentum principles.
Core Solution Summary:
-
Geometry Setup: Define the geometry with fixed points A and B, 8l apart, and string segments of length 5l each. The bead forms an isosceles triangle.
-
Equilibrium Analysis: In equilibrium, the vertical components of the tensions balance the weight mg. This leads to: T0=3031mg
-
Post-Impulse Analysis: After the bead receives a horizontal velocity 2gl, the net force (vector sum of tensions) has a component perpendicular to the velocity, causing centripetal acceleration. This gives: r0=335l
