Question

A wave is represented by the equation

$y = A \sin(10\pi x + 15\pi t + \frac{\pi}{3})$ where

'x' is in metre and 't' is in second. The expression represents a wave travelling in the

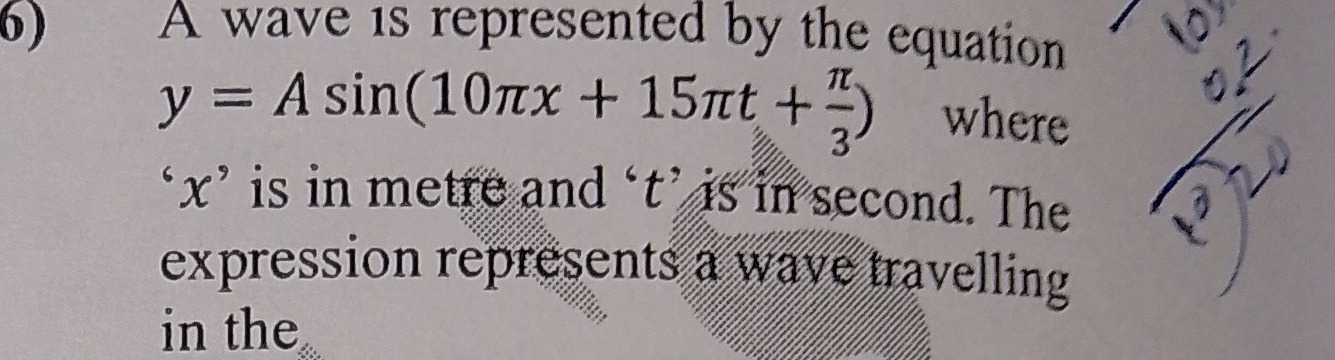
• A. positive x direction
• B. negative x direction
• C. positive y direction
• D. negative y direction

Answer 1

Answer: (B)

negative x direction

Answer 2

The wave is given by

$$y = A \sin(10\pi x + 15\pi t + \tfrac{\pi}{3}).$$

A standard traveling wave in the $+x$ direction is written as

$$y = A \sin(kx - \omega t + \phi).$$

Here, the sign before $t$ is positive, i.e., the phase is

$$10\pi x + 15\pi t + \tfrac{\pi}{3} = 10\pi\left(x + \frac{3}{2}t\right)+ \tfrac{\pi}{3}.$$

This represents a wave of the form $\sin[k(x+vt)+\phi]$ that travels in the negative $x$ direction.