Question

A uniform string of length L and total mass M is suspended vertically and a transverse pulse is given at the top end of it. At the same moment a body is released from rest and falls freely from the top of the string. How far from the bottom does the body pass the pulse.

Answer 1

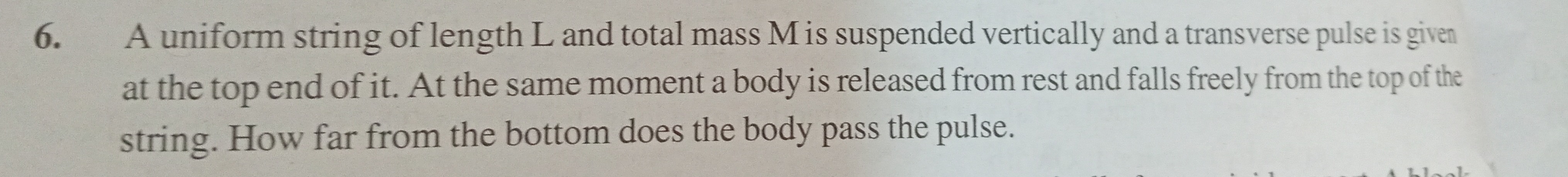
L/9

Answer 2

The string has length L and mass M, suspended vertically. The linear mass density is $\mu = M/L$.

Consider a point on the string at a distance x from the top end (0 $\le$ x $\le$ L). The portion of the string below this point has length L-x and mass $\mu(L-x)$. The tension at this point is $T(x) = \mu(L-x)g = (M/L)(L-x)g$.

The speed of a transverse pulse on the string at position x is $v(x) = \sqrt{\frac{T(x)}{\mu}} = \sqrt{\frac{(M/L)(L-x)g}{M/L}} = \sqrt{(L-x)g}$.

The pulse is traveling downwards, so its velocity is $\frac{dx}{dt} = \sqrt{(L-x)g}$.

To find the time $t_p$ for the pulse to travel from the top (x=0) to a position x, we integrate: $\int_{0}^{t_p} dt = \int_{0}^{x} \frac{dx}{\sqrt{(L-x)g}}$

$t_p = \frac{1}{\sqrt{g}} \int_{0}^{x} (L-x)^{-1/2} dx$

Let $u = L-x$, so $du = -dx$. When $x=0$, $u=L$. When $x=x$, $u=L-x$.

$t_p = \frac{1}{\sqrt{g}} \int_{L}^{L-x} u^{-1/2} (-du) = \frac{1}{\sqrt{g}} \int_{L-x}^{L} u^{-1/2} du$

$t_p = \frac{1}{\sqrt{g}} [2u^{1/2}]_{L-x}^{L} = \frac{2}{\sqrt{g}} (\sqrt{L} - \sqrt{L-x})$.

A body is released from rest from the top end (x=0) at the same moment (t=0). The body falls freely under gravity. The position of the body at time t is given by $x_b(t) = \frac{1}{2}gt^2$, where x is the distance from the top.

The body passes the pulse when they are at the same position x at the same time t. Let this time be $t$. The position of the pulse at time t is x, where t is the time taken for the pulse to reach x, i.e., $t = t_p$. So, the meeting condition is $x_b(t) = x$.

$\frac{1}{2}gt^2 = x$.

The time taken is $t = \sqrt{\frac{2x}{g}}$.

Equating the time taken for the pulse to reach x and the time taken for the body to fall x:

$\frac{2}{\sqrt{g}} (\sqrt{L} - \sqrt{L-x}) = \sqrt{\frac{2x}{g}}$

Multiply both sides by $\sqrt{g}$:

$2 (\sqrt{L} - \sqrt{L-x}) = \sqrt{2x}$

Square both sides:

$4 (\sqrt{L} - \sqrt{L-x})^2 = 2x$

$2 (L + (L-x) - 2\sqrt{L(L-x)}) = x$

$2 (2L - x - 2\sqrt{L^2 - Lx}) = x$

$4L - 2x - 4\sqrt{L^2 - Lx} = x$

$4L - 3x = 4\sqrt{L^2 - Lx}$

Square both sides again:

$(4L - 3x)^2 = 16 (L^2 - Lx)$

$16L^2 - 24Lx + 9x^2 = 16L^2 - 16Lx$

$9x^2 - 24Lx + 16Lx = 0$

$9x^2 - 8Lx = 0$

$x(9x - 8L) = 0$

This gives two solutions: $x=0$ or $x = \frac{8L}{9}$.

$x=0$ corresponds to the initial position at $t=0$. The meeting point during the motion is $x = \frac{8L}{9}$.

This is the distance from the top end. The question asks for the distance from the bottom end. Distance from the bottom = L - x = $L - \frac{8L}{9} = \frac{9L - 8L}{9} = \frac{L}{9}$.